
【題目】在矩形ABCD中,點P在AD上,AB=2,AP=1.將直角尺的頂點放在P處,直角尺的兩邊分別交AB,BC于點E,F,連接EF(如圖①).
(1)當點E與點B重合時,點F恰好與點C重合(如圖②),求PC的長;
(2)探究:將直尺從圖②中的位置開始,繞點P順時針旋轉,當點E和點A重合時停止.在這個過程中,請你觀察、猜想,并解答:
①tan∠PEF的值是否發生變化?請說明理由;
②直接寫出從開始到停止,線段EF的中點經過的路線長.
【答案】
(1)解:在矩形ABCD中,
∠A=∠D=90°,
AP=1,CD=AB=2,則PB= ![]() ,
,
∴∠ABP+∠APB=90°,
又∵∠BPC=90°,
∴∠APB+∠DPC=90°,
∴∠ABP=∠DPC,
∴△APB∽△DCP,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴PC=2 ![]()
(2)解:①tan∠PEF的值不變.
理由:過F作FG⊥AD,垂足為G,
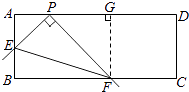
則四邊形ABFG是矩形,
∴∠A=∠PGF=90°,GF=AB=2,
∴∠AEP+∠APE=90°,
又∵∠EPF=90°,
∴∠APE+∠GPF=90°,
∴∠AEP=∠GPF,
∴△APE∽△GPF,
∴ ![]() =
= ![]() =
= ![]() =2,
=2,
∴Rt△EPF中,tan∠PEF= ![]() =2,
=2,
∴tan∠PEF的值不變;
②設線段EF的中點為O,連接OP,OB,
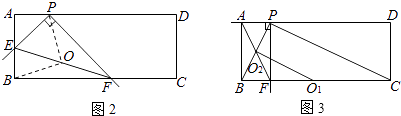
∵在Rt△EPF中,OP= ![]() EF,
EF,
在Rt△EBF中,OB= ![]() EF,
EF,
∴OP=OB= ![]() EF,
EF,
∴O點在線段BP的垂直平分線上,
∴線段EF的中點經過的路線長為O1O2= ![]() PC=
PC= ![]()
【解析】1)由勾股定理求PB,利用互余關系證明△APB∽△DCP,利用相似比求PC;
(2)①tan∠PEF的值不變.過F作FG⊥AD,垂足為G,同(1)的方法證明△APB∽△DCP,得相似比,再利用銳角三角函數的定義求值;
②如圖3,畫出起始位置和終點位置時,線段EF的中點O1,O2,連接O1O2,線段O1O2即為線段EF的中點經過的路線長,也就是△BPC的中位線.
【考點精析】解答此題的關鍵在于理解勾股定理的概念的相關知識,掌握直角三角形兩直角邊a、b的平方和等于斜邊c的平方,即;a2+b2=c2,以及對三角形中位線定理的理解,了解連接三角形兩邊中點的線段叫做三角形的中位線;三角形中位線定理:三角形的中位線平行于三角形的第三邊,且等于第三邊的一半.


 課程達標測試卷闖關100分系列答案
課程達標測試卷闖關100分系列答案 新卷王期末沖刺100分系列答案
新卷王期末沖刺100分系列答案 全能闖關100分系列答案
全能闖關100分系列答案科目:初中數學 來源: 題型:
【題目】我國古代數學的許多創新和發展都位居世界前列,如南宋數學家楊輝揭示了二項和![]() 的展開式的各項系數規律,比歐洲的發現早三百年,為紀念楊輝的功績,世人稱如圖中右圖叫“楊輝三角”。
的展開式的各項系數規律,比歐洲的發現早三百年,為紀念楊輝的功績,世人稱如圖中右圖叫“楊輝三角”。
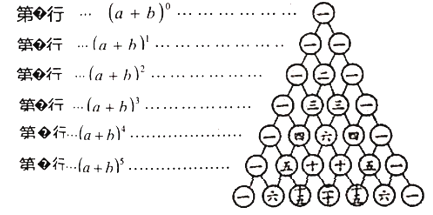
(1)觀察“楊輝三角”規律,依次寫出“楊輝三角”第![]() 行中從左到右的各數;
行中從左到右的各數;
(2)請運用冪的意義和多項式乘法法則,按如下要求展開下列各式,以驗證“楊輝三角”第四行的規律:展開后各項按字母![]() 降冪、
降冪、![]() 升冪排列
升冪排列![]()
(3)解不等式![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC,∠A=70°,D、E、F分別在BC、AC、AB上,且∠1=∠2,∠3=∠4,則∠EDF等于( )

A. 70°B. 65°C. 55°D. 45°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一只不透明的箱子里共有3個球,其中2個白球,1個紅球,它們除顏色外均相同.
(1)從箱子中隨機摸出一個球是白球的概率是多少?
(2)從箱子中隨機摸出一個球,記錄下顏色后不將它放回箱子,攪勻后再摸出一個球,求兩次摸出的球都是白球的概率,并畫出樹狀圖.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,如果以正方形ABCD的對角線AC為邊作第二個正方形ACEF,再以對角線AE為邊作第三個正方形AEGH,如此下去,……,已知正方形ABCD的面積為S1為1,按上述方法所作的正方形的面積依次為S2,S3,……………,則Sn(n為正整數),那么第n個正方形的面積Sn等于( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC是⊙O的內接三角形,AC是⊙O的直徑,∠C=50°,∠ABC的平分線BD交⊙O于點D,則∠BAD的度數是( )
A.45°
B.85°
C.90°
D.95°
查看答案和解析>>
科目:初中數學 來源: 題型:
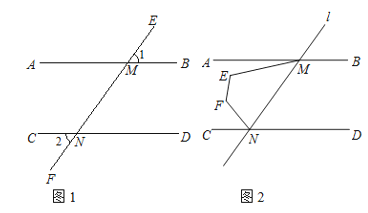
【題目】如圖,直線l分別交AB,CD于點M,N(點M在點N的右側),若∠1=∠2
(1)求證:AB//CD;
(2)如圖,點E、F在AB,CD之間,且在MN的左側,若∠MEF+∠EFN=255°,求∠AME+∠FNC的度數;
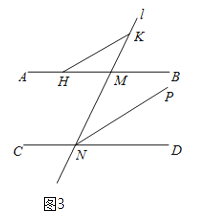
(3)如圖,點H在直線AB上,且位于點M的左側;點K在直線MN上,且在直線AB的上方.點Q在∠MND的角平分線NP上,且∠KHM=2∠MHQ,若∠HQN+∠HKN=75°,直接寫出∠PND和∠QHB的數量關系.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:![]() 中,
中,![]() ,
,![]() ,點
,點![]() 為
為![]() 內一點,連接
內一點,連接![]() ,
,![]() ,
,![]() ,過點
,過點![]() 作
作![]() ,交
,交![]() 的延長線于點
的延長線于點![]() .
.


(1)如圖1,求證:![]() ;
;
(2)如圖2,點![]() 為
為![]() 的中點,分別連接
的中點,分別連接![]() ,
,![]() ,求
,求![]() 的度數;
的度數;
(3)如圖3,在(2)的條件下,點![]() 為
為![]() 上一點,連接
上一點,連接![]() ,點
,點![]() 為
為![]() 的中點,連接
的中點,連接![]() ,過點
,過點![]() 作
作![]() ,交
,交![]() 的延長線于點
的延長線于點![]() ,若
,若![]() ,
,![]() 的面積為30,
的面積為30,![]() ,求線段
,求線段![]() 的長.
的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com