
【題目】在平面直角坐標系![]() 中,已知拋物線
中,已知拋物線![]() .
.
(1)當![]() 時,
時,
①拋物線![]() 的對稱軸為
的對稱軸為![]() ________;
________;
②若在拋物線![]() 上有兩點
上有兩點![]() ,且
,且![]() ,則
,則![]() 的取值范圍是________;
的取值范圍是________;
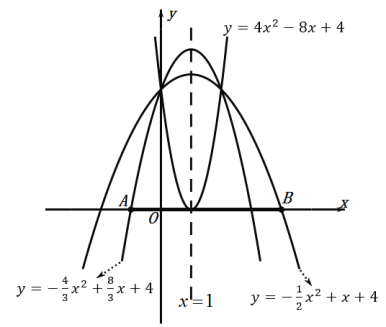
(2)拋物線![]() 的對稱軸與
的對稱軸與![]() 軸交于點
軸交于點![]() ,點
,點![]() 與點
與點![]() 關于
關于![]() 軸對稱,將點
軸對稱,將點![]() 向右平移3個單位得到點
向右平移3個單位得到點![]() ,若拋物線
,若拋物線![]() 與線段
與線段![]() 恰有一個公共點,結合圖象,求
恰有一個公共點,結合圖象,求![]() 的取值范圍.
的取值范圍.
【答案】(1)①1;②![]() 或
或![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
(1)①根據拋物線的對稱軸公式即可求得;
②根據拋物線的對稱性質,求得點![]() 的對稱點為
的對稱點為![]() ,根據函數圖象即可求得答案;
,根據函數圖象即可求得答案;
(2)根據平移的性質,分別求得A、B的坐標,依題意,根據函數圖象,三種情況分類討論,得出相應的a值,從而得結論.
(1)①拋物線![]() 的對稱軸為:
的對稱軸為:![]() ;
;
②∵拋物線![]() 關于
關于![]() 對稱,
對稱,
∴點![]() 的對稱點為
的對稱點為![]() ,
,
∵![]() ,
,
∴拋物線![]() 開口向上,
開口向上,
觀察圖象,![]() 或
或![]() 時,
時,![]() ;
;
故答案為:①1;②![]() 或
或![]() ;
;
(2)∵拋物線![]() 的對稱軸為
的對稱軸為![]() ,且對稱軸與
,且對稱軸與![]() 軸交于點
軸交于點![]() ,
,
∴點![]() 的坐標為
的坐標為![]() ,
,
∵點![]() 與點
與點![]() 關于
關于![]() 軸對稱,
軸對稱,
∴點![]() 的坐標為
的坐標為![]() ,
,
∵點![]() 右移3個單位得到點
右移3個單位得到點![]() ,
,
∴點![]() 的坐標為
的坐標為![]() ,
,
依題意,拋物線![]() 與線段
與線段![]() 恰有一個公共點,
恰有一個公共點,
把點![]() 代入
代入![]() 可得
可得![]() ;
;
把點![]() 代入
代入![]() 可得
可得![]() ;
;
把點![]() 代入
代入![]() 可得
可得![]() .
.
根據所畫圖象可知拋物線![]() 與線段
與線段![]() 恰有一個公共點時可得
恰有一個公共點時可得![]() 或
或![]() .
.


科目:初中數學 來源: 題型:
【題目】近年來,移動支付已成為主要支付方式之一.為了解某校800名學生上個月A,B兩種移動支付方式的使用情況,從全校學生中隨機抽取了100人,發現樣本中A,B兩種支付方式都不使用的有5人,樣本中僅使用A和僅使用B的學生的支付金額分布情況如下:
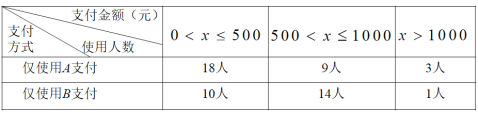
下面有四個推斷:
①從全校學生中隨機抽取1人,該學生上個月僅使用A支付的概率為0.3;
②從全校學生中隨機抽取1人,該學生上個月A,B兩種支付方式都使用的概率為0.45;
③估計全校僅使用B支付的學生人數為200人;
④這100名學生中,上個月僅使用A和僅使用B支付的學生支付金額的中位數為800元.
其中合理推斷的序號是( )
A.①②B.①③C.①④D.②③
查看答案和解析>>
科目:初中數學 來源: 題型:
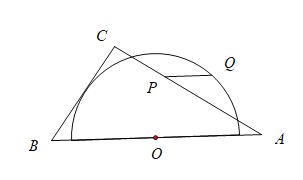
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,以邊
,以邊![]() 的中點
的中點![]() 為圓心作半圓,使
為圓心作半圓,使![]() 與半圓相切,點
與半圓相切,點![]() 分別是邊
分別是邊![]() 和半圓上的動點,連接
和半圓上的動點,連接![]() ,則
,則![]() 長的最大值與最小值的和是( )
長的最大值與最小值的和是( )
A.8B.9C.10D.12
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一艘輪船從位于燈塔C的北偏東60°方向,距離燈塔60 n mile的小島A出發,沿正南方向航行一段時間后,到達位于燈塔C的南偏東45°方向上的B處,這時輪船B與小島A的距離是( )

A.![]() n mileB.60 n mileC.120 n mileD.
n mileB.60 n mileC.120 n mileD.![]() n mile
n mile
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某數學活動小組為測量學校旗桿AB的高度,沿旗桿正前方![]() 米處的點C出發,沿斜面坡度
米處的點C出發,沿斜面坡度![]() 的斜坡CD前進4米到達點D,在點D處安置測角儀,測得旗桿頂部A的仰角為37°,量得儀器的高DE為1.5米.已知A、B、C、D、E在同一平面內,AB⊥BC,AB//DE.求旗桿AB的高度.(參考數據:sin37°≈
的斜坡CD前進4米到達點D,在點D處安置測角儀,測得旗桿頂部A的仰角為37°,量得儀器的高DE為1.5米.已知A、B、C、D、E在同一平面內,AB⊥BC,AB//DE.求旗桿AB的高度.(參考數據:sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() .計算結果保留根號)
.計算結果保留根號)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某玩具商店以每件60元為成本購進一批新型玩具,以每件100元的價格銷售則每天可賣出20件,為了擴大銷售,增加盈利,盡快減少庫存,商店決定采取適當的降價措施,經調查發現:若每件玩具每降價1元,則每天可多賣2件.
(1)若商店打算每天盈利1200元,每件玩具的售價應定為多少元?
(2)若商店為追求效益最大化,每件玩具的售價定為多少元時,商店每天盈利最多?最多盈利多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
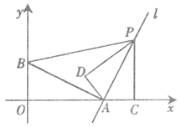
【題目】如圖,在直角坐標系中,點![]() ,點
,點![]() ,過點
,過點![]() 的直線
的直線![]() 垂直于線段
垂直于線段![]() ,點
,點![]() 是直線
是直線![]() 上在第一象限內的一動點,過點
上在第一象限內的一動點,過點![]() 作
作![]() 軸,垂足為
軸,垂足為![]() ,把
,把![]() 沿
沿![]() 翻折
翻折![]() ,使點
,使點![]() 落在點
落在點![]() 處,若以
處,若以![]() ,
,![]() ,
,![]() 為頂點的三角形與△ABP相似,則滿足此條件的點
為頂點的三角形與△ABP相似,則滿足此條件的點![]() 的坐標為__________.
的坐標為__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】探究問題:
⑴方法感悟:
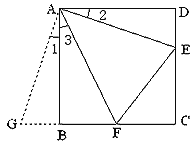
如圖①,在正方形ABCD中,點E,F分別為DC,BC邊上的點,且滿足∠EAF=45°,連接EF,求證DE+BF=EF.
感悟解題方法,并完成下列填空:
將△ADE繞點A順時針旋轉90°得到△ABG,此時AB與AD重合,由旋轉可得:
AB=AD,BG=DE, ∠1=∠2,∠ABG=∠D=90°,
∴∠ABG+∠ABF=90°+90°=180°,
因此,點G,B,F在同一條直線上.
∵∠EAF=45°
∴∠2+∠3=∠BAD-∠EAF=90°-45°=45°.
∵∠1=∠2,
∴∠1+∠3=45°.
即∠GAF=∠_________.
又AG=AE,AF=AF
∴△GAF≌_______.
∴_________=EF,故DE+BF=EF.
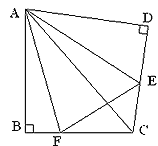
⑵方法遷移:
如圖②,將![]() 沿斜邊翻折得到△ADC,點E,F分別為DC,BC邊上的點,且∠EAF=
沿斜邊翻折得到△ADC,點E,F分別為DC,BC邊上的點,且∠EAF=![]() ∠DAB.試猜想DE,BF,EF之間有何數量關系,并證明你的猜想.
∠DAB.試猜想DE,BF,EF之間有何數量關系,并證明你的猜想.
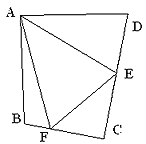
⑶問題拓展:
如圖③,在四邊形ABCD中,AB=AD,E,F分別為DC,BC上的點,滿足![]() ,試猜想當∠B與∠D滿足什么關系時,可使得DE+BF=EF.請直接寫出你的猜想(不必說明理由)
,試猜想當∠B與∠D滿足什么關系時,可使得DE+BF=EF.請直接寫出你的猜想(不必說明理由)
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com