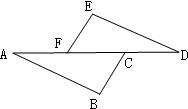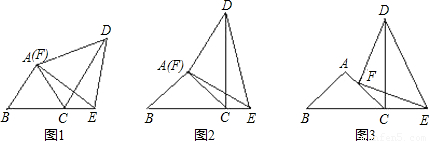
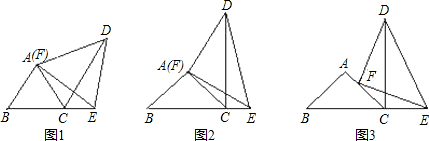
解:(1)∵AB=AC,FD=FE,∠BAC=∠DFE=60°,
∴△ABC與△FED是等邊三角形,
∴∠ABC=∠ACB=60°,
又∵∠BAC=∠DFE=60°,
∴∠BAC+∠CAE=∠DFE+∠CAE,
即∠BAE=∠CFD,
在△BAE和△CFD中
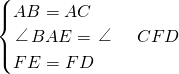
,
∴△BAE≌△CFD(SAS),
∴∠ABE=∠FCD=60°,
∴∠DCE=180°-∠ACB-∠FCD=60°;
(2)∵AB=AC,∠BAC=95°,
∴∠ABC=∠ACB=42.5°
又∵∠BAC=∠DFE,
∴∠BAC+∠CAE=∠DFE+∠CAE,
即∠BAE=∠CFD,
在△BAE和△CFD中
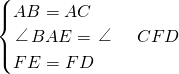
,
∴△BAE≌△CFD(SAS),
∴∠ABE=∠FCD=42.5°,
∴∠DCE=180°-∠ACB-∠FCD=95°;
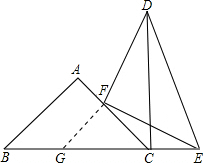
(3)過F作FG∥AB,
∴∠FGC=∠ABC,
又AB=AC,
∴∠ABC=∠ACB,
∴∠FGC=∠ACB,∴FG=FC,
又∠BAC=n°,
∴∠ABC=∠ACB=
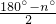
,
又∵FG∥AB,
∴∠CFG=∠CAB,又∠CAB=∠DFE,
∴∠CFG=∠DFE,
∴∠CFG+∠EFC=∠DFE+∠EFC,
即∠GFE=∠CFD,
在△GFE和△CFD中
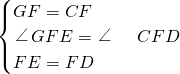
,
∴△GFE≌△CFD(SAS),
∴∠FGC=∠FCD=
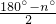
,
∴∠DCE=180°-∠ACB-∠FCD
=180°-
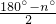
-
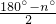
=n°.
分析:(1)由AB=AC,FD=FE,再加上∠BAC=∠DFE=60°,根據有一個角是60°的等腰三角形為等邊三角形得到三角形ABC和三角形FDE都為等邊三角形,從而得到∠BAC與∠EAD相等都為60°,兩角都加上∠ACE,根據等式的基本性質得到一對角相等,利用SAS即可得到三角形ABE與三角形ACD全等,根據全等三角形的對應角相等得到∠ACD=∠B=60°,又∠ACB也為60°,根據平角定義即可求出∠DCE為60°;
(2)由∠BAC與∠EAD相等都為95°,兩角都加上∠ACE,根據等式的基本性質得到一對角相等,再由AB=AC,FD=FE,利用SAS得到三角形ABE與三角形ACD全等,根據全等三角形的對應角相等得到∠ACD=∠B=∠C=

,由平角定義即可求出∠DCE的度數;
(3)過F作FG平行與AB,由兩直線平行得到兩對同位角相等,先根據等量代換得到∠FGC=∠ACB,利用等角對等邊得到FG=FC,再等量代換得到∠CFG=∠DFE,兩角都加上∠CFE,根據等式的基本性質得到一對角相等,再由FG=FC,FD=FE,利用SAS得到三角形GFE與三角形CFD全等,根據全等三角形的對應角相等得到∠FGC=∠FDC=
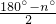
,由平角定義即可求出∠DCE的度數.
點評:此題考查了全等三角形的判定與性質,等邊三角形的性質及等腰三角形的性質,解題時采用了由特殊到一般的推理方法:發現規律并證明,要注意思路及方法的遷移,同時通過構造全等三角形來解決證明角、邊的相等問題,尤其在證明其性質和判定中,展示的轉化意識對學生分析和解決問題能力的提高有非常重要的價值.本題第三問作出輔助線FG平行于AB是證明的突破點.

 解:(1)∵AB=AC,FD=FE,∠BAC=∠DFE=60°,
解:(1)∵AB=AC,FD=FE,∠BAC=∠DFE=60°,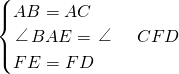 ,
,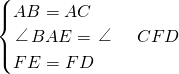 ,
,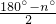 ,
,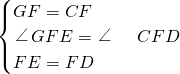 ,
,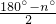 ,
,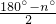 -
-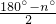 =n°.
=n°. ,由平角定義即可求出∠DCE的度數;
,由平角定義即可求出∠DCE的度數;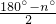 ,由平角定義即可求出∠DCE的度數.
,由平角定義即可求出∠DCE的度數.

 18、已知△ABC,利用直尺和圓規,根據下列要求作圖(保留作圖痕跡,不要求寫作法),并根據要求填空:
18、已知△ABC,利用直尺和圓規,根據下列要求作圖(保留作圖痕跡,不要求寫作法),并根據要求填空: