
【題目】已知,四邊形ABCD內(nèi)接于![]() ,對角線AC和BD相交于點E,AC是
,對角線AC和BD相交于點E,AC是![]() 的直徑.
的直徑.
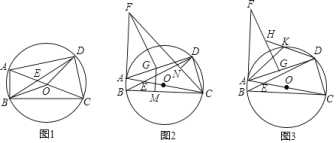
![]() 如圖1,連接OB和OD,求證:
如圖1,連接OB和OD,求證:![]() ;
;
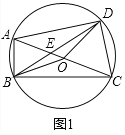
![]() 如圖2,延長BA到點F,使
如圖2,延長BA到點F,使![]() ,在AD上取一點G,使
,在AD上取一點G,使![]() ,連接FG和FC,過點G作
,連接FG和FC,過點G作![]() ,垂足為M,過點D作
,垂足為M,過點D作![]() ,垂足為N,求
,垂足為N,求![]() 的值;
的值;
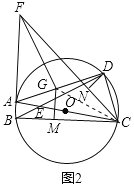
![]() 如圖3,在
如圖3,在![]() 的條件下,點H為FG的中點,連接DH交
的條件下,點H為FG的中點,連接DH交![]() 于點K,連接AK,若
于點K,連接AK,若![]() ,
,![]() ,求線段BC的長.
,求線段BC的長.
【答案】(1)證明見解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)利用圓周角定理得到∠AOB=2∠ACB,∠COD=2∠DBC,得用三角形的外角定理得到∠ACB+∠DBC=∠AEB,從而得到結(jié)論;
(2)連接GC,先證明∠MCG=∠NCD,得到![]() ;
;
(3)先證![]() ≌
≌![]() ,再證
,再證![]() ≌
≌![]() ,設(shè)PQ=a,PD=7a,可求出QD=
,設(shè)PQ=a,PD=7a,可求出QD=![]() a,RQ=
a,RQ=![]() a,利用三角函數(shù)關(guān)系即可求解.
a,利用三角函數(shù)關(guān)系即可求解.
![]() 證明:如圖1中,
證明:如圖1中,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() 如圖2中,連接GC.
如圖2中,連接GC.
![]() 是直徑,
是直徑,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() 如圖3中,延長DH到T,使得
如圖3中,延長DH到T,使得![]() ,連接TF,TB,CK,作
,連接TF,TB,CK,作![]() 于P交AD于點Q,作
于P交AD于點Q,作![]() 于R.
于R.

![]() 點H是FG的中點,
點H是FG的中點,
![]() ,
,
![]() ,
,![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 是等腰直角三角形,
是等腰直角三角形,
![]() ,
,
![]() ,設(shè)
,設(shè)![]() ,
,![]() ,
,
在![]() 中,可得
中,可得![]() ,
,
![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,設(shè)
,設(shè)![]() ,
,![]() ,則
,則![]() ,
,
![]() ,
,
![]() .
.
故答案為:(1)證明見解析;(2)![]() ;(3)
;(3)![]() .
.


科目:初中數(shù)學(xué) 來源: 題型:
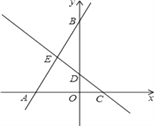
【題目】如圖,在平面直角坐標系中,點O為坐標原點,直線y=﹣x+b與坐標軸交于C,D兩點,直線AB與坐標軸交于A,B兩點,線段OA,OC的長是方程x2﹣3x+2=0的兩個根(OA>OC).
(1)求點A,C的坐標;
(2)直線AB與直線CD交于點E,若點E是線段AB的中點,反比例函數(shù)y=![]() (k≠0)的圖象的一個分支經(jīng)過點E,求k的值;
(k≠0)的圖象的一個分支經(jīng)過點E,求k的值;
(3)在(2)的條件下,點M在直線CD上,坐標平面內(nèi)是否存在點N,使以點B,E,M,N為頂點的四邊形是菱形?若存在,請直接寫出滿足條件的點N的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,四邊形ABCD是矩形,把矩形沿AC折疊,點B落在點E處,AE與DC的交點為O,連接DE.
(1)求證:△ADE≌△CED;
(2)求證:DE∥AC.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】我們知道,直線與圓有三種位置關(guān)系:相交、相切、相離.類比直線與圓的位置關(guān)系,給出如下定義:與坐標軸不平行的直線與拋物線有兩個公共點叫做直線與拋物線相交;直線與拋物線有唯一的公共點叫做直線與拋物線相切,這個公共點叫做切點;直線與拋物線沒有公共點叫做直線與拋物線相離.
(1)記一次函數(shù)![]() 的圖像為直線
的圖像為直線![]() ,二次函數(shù)
,二次函數(shù)![]() 的圖像為拋物線
的圖像為拋物線![]() ,若直線
,若直線![]() 與拋物線
與拋物線![]() 相交,求
相交,求![]() 的取值范圍;
的取值范圍;
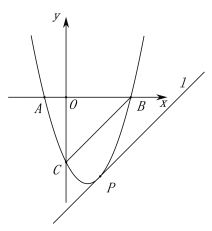
(2)若二次函數(shù)![]() 的圖像與
的圖像與![]() 軸交于點
軸交于點![]() 、
、![]() ,與
,與![]() 軸交于點
軸交于點![]() ,直線l與CB平行,并且與該二次函數(shù)的圖像相切,求切點P的坐標.
,直線l與CB平行,并且與該二次函數(shù)的圖像相切,求切點P的坐標.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
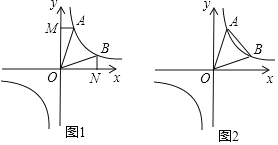
【題目】反比例函數(shù)![]() 在第一象限上有兩點A,B.
在第一象限上有兩點A,B.
(1)如圖1,AM⊥y軸于M,BN⊥x軸于N,求證:△AMO的面積與△BNO面積相等;
(2)如圖2,若點A(2,m),B(n,2)且△AOB的面積為16,求k值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】有3張正面分別寫有數(shù)字![]() ,0,1的卡片,它們的背面完全相同,現(xiàn)將這3張卡片背面朝上洗勻,小明先從中任意抽出一張卡片記下數(shù)字為x;小亮再從剩下的卡片中任意取出一張記下數(shù)字為y,記作
,0,1的卡片,它們的背面完全相同,現(xiàn)將這3張卡片背面朝上洗勻,小明先從中任意抽出一張卡片記下數(shù)字為x;小亮再從剩下的卡片中任意取出一張記下數(shù)字為y,記作![]() .
.
![]() 用列表或畫樹狀圖的方法列出所有可能的點P的坐標;
用列表或畫樹狀圖的方法列出所有可能的點P的坐標;
![]() 若規(guī)定:點
若規(guī)定:點![]() 在第二象限小明獲勝;點
在第二象限小明獲勝;點![]() 在第四象限小亮獲勝,游戲規(guī)則公平嗎?
在第四象限小亮獲勝,游戲規(guī)則公平嗎?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
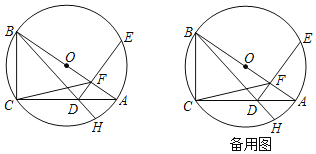
【題目】如圖,![]() 是
是![]() 的內(nèi)接三角形,AB為
的內(nèi)接三角形,AB為![]() 直徑,
直徑,![]() ,
,![]() ,點D為線段AC上一動點,過點D作AB的垂線交
,點D為線段AC上一動點,過點D作AB的垂線交![]() 于點E,交AB于點F,連結(jié)BD,CF,并延長BD交
于點E,交AB于點F,連結(jié)BD,CF,并延長BD交![]() 于點H.
于點H.
![]() 求
求![]() 的半徑;
的半徑;
![]() 當DE經(jīng)過圓心O時,求AD的長;
當DE經(jīng)過圓心O時,求AD的長;
![]() 求證:
求證:![]() ;
;
![]() 求
求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,拋物線y=ax2+bx-4a經(jīng)過A(-1,0)、C(0,4)兩點,與x軸交于另一點B.
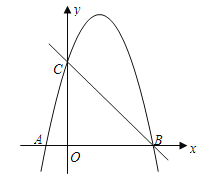
(1)求拋物線的解析式;
(2)已知點D(m,m+1)在第一象限的拋物線上,求點D關(guān)于直線BC對稱的點的坐標;
(3)在(2)的條件下,連接BD,點P為拋物線上一點,且∠DBP=45°,求點P的坐標.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com