【題目】已知，AB和AC是
的兩條弦，
，M、N分別是AB、AC的中點，則
的度數(shù)為______．
【答案】
或
【解析】
連接OM，ON，利用垂徑定理得OM⊥AB，ON⊥AC，再分類討論，當(dāng)AB，AC在圓心異側(cè)時（如圖1），利用四邊形內(nèi)角和得結(jié)果；當(dāng)AB，AC在圓心同側(cè)時（如圖2），利用相似三角形的性質(zhì)得結(jié)果．
解：連接OM，ON，
∵M、N分別是AB和AC的中點，
∴OM⊥AB，ON⊥AC，
當(dāng)AB，AC在圓心異側(cè)時（如圖1），
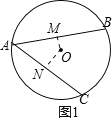
∵∠BAC=57°，
在四邊形AMON中，
∴∠MON=360°﹣90°﹣90°﹣57°=123°；
當(dāng)AB，AC在圓心同側(cè)時（如圖2），
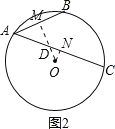
∵∠ADM=∠ODN，∠AMD=∠OND，
∴△ADM∽△ODN，
∴∠MON=∠BAC=57°．
故答案為：123°或57°．
科目：初中數(shù)學(xué) 來源： 題型：
【題目】如圖1，將兩個完全相同的三角形紙片ABC和DEC重合放置，其中∠C=900，∠B=∠E=300.
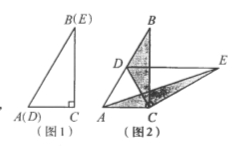
（1）操作發(fā)現(xiàn)如圖2，固定△ABC，使△DEC繞點C旋轉(zhuǎn)。當(dāng)點D恰好落在BC邊上時，填空：線段DE與AC的位置關(guān)系是 ；
② 設(shè)△BDC的面積為S1，△AEC的面積為S2。則S1與S2的數(shù)量關(guān)系是 。
（2）猜想論證
當(dāng)△DEC繞點C旋轉(zhuǎn)到圖3所示的位置時，小明猜想（1）中S1與S2的數(shù)量關(guān)系仍然成立，并嘗試分別作出了△BDC和△AEC中BC，CE邊上的高，請你證明小明的猜想。
（3）拓展探究
已知∠ABC=600，點D是其角平分線上一點，BD=CD=4，OE∥AB交BC于點E（如圖4），若在射線BA上存在點F，使S△DCF =S△BDC,請直接寫出相應(yīng)的BF的長
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】有下列四個條件：①AB=BC，②∠ABC=90
，③AC=BD，④AC⊥BD．從中選取兩個作為補充條件，使□BCD為正方形（如圖）．現(xiàn)有下列四種選法，其中錯誤的是 ( )
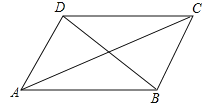
A. ②③ B. ②④ C. ①② D. ①③
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】某校同學(xué)組織了一次經(jīng)典朗讀比賽，甲、乙兩隊各10人的比賽成績?nèi)缦卤恚?/span>10分制）：
甲 |
|
|
|
|
|
|
|
|
|
|
乙 |
|
|
|
|
|
|
|
|
|
|
（1）甲隊成績的中位數(shù)是 分，乙隊成績的眾數(shù)是 分；
（2）計算乙隊的平均成績和方差；
（3）已知甲隊成績的方差是
分2，則成績較為整齊的是 隊．
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
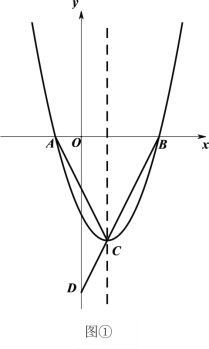
【題目】如圖①，二次函數(shù)
的圖像與
軸交于
、
兩點（點在的左側(cè)），頂點為
，連接
并延長交
軸于點
，若
.
（1）求二次函數(shù)的表達(dá)式；
（2）在軸上方有一點
，
，且
，連接
并延長交拋物線于點
，求點的坐標(biāo)；
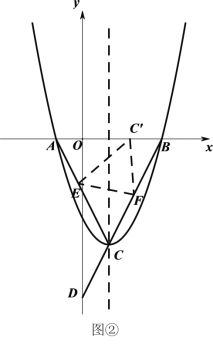
（3）如圖②，折疊△
，使點落在線段
上的點
處，折痕為
．若△
有一條邊與軸垂直，直接寫出此時點的坐標(biāo)．
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
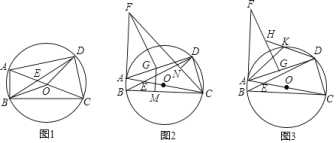
【題目】已知，四邊形ABCD內(nèi)接于
，對角線AC和BD相交于點E，AC是的直徑．
如圖1，連接OB和OD，求證：
；
如圖2，延長BA到點F，使
，在AD上取一點G，使
，連接FG和FC，過點G作
，垂足為M，過點D作
，垂足為N，求
的值；
如圖3，在的條件下，點H為FG的中點，連接DH交于點K，連接AK，若
，
，求線段BC的長．
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
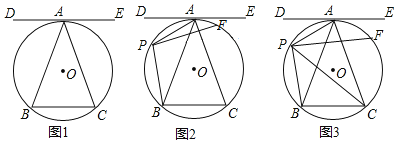
【題目】.如圖，⊙O是△ABC的外接圓，直線DE是⊙O的切線，點A為切點，DE∥BC；
（1）如圖1.求證：AB=AC；
（2）如圖2.點P是弧AB上一動點，連接PA、PB，作PF⊥PB,垂足為點P,PF交⊙O于點F, 求證：∠BAC=2∠APF；
（3）如圖3.在（2）的條件下，連接PC，PA=
，PB=
，PC=
，求線段PF的長.
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
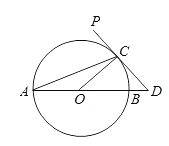
【題目】如圖，AB 為⊙O 的直徑，PD 切⊙O 于點 C，交 AB 的延長線于點 D，且∠D=2∠A.
（1）求∠D 的度數(shù)；
（2)若⊙O 的半徑為 m，求 BD 的長.
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
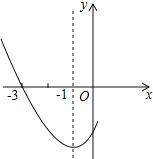
【題目】如圖，是二次函數(shù)
圖象的一部分，其對稱軸是
，且過點
，下列說法：
；
；
；
若
，
是拋物線上兩點，則
，其中正確的有
A. 1個
B. 2個
C. 3個
D. 4個
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
