
【題目】如圖,一次函數y=x+m的圖象與反比例函數y= ![]() 的圖象交于A,B兩點,且與x軸交于點C,點A的坐標為(2,1).
的圖象交于A,B兩點,且與x軸交于點C,點A的坐標為(2,1). 
(1)求一次函數和反比例函數的解析式;
(2)求點C的坐標;
(3)結合圖象直接寫出不等式0<x+m≤ ![]() 的解集.
的解集.
【答案】
(1)解:∵一次函數y=x+m的圖象與反比例函數y= ![]() 的圖象交于A,B兩點,點A的坐標為(2,1),
的圖象交于A,B兩點,點A的坐標為(2,1),
∴1=2+m,解得m=﹣1,
1= ![]() ,解得k=﹣2.
,解得k=﹣2.
故一次函數的解析式為y=x﹣1,反比例函數的解析式為y= ![]() ;
;
(2)解:令y=0,則0=x﹣1,解得x=1.
故點C的坐標為(1,0)
(3)解:觀察函數圖象得到不等式0<x+m≤ ![]() 的解集為1<x≤2
的解集為1<x≤2
【解析】(1)先把A(2,1)代入y=x+m得到m=﹣1,再把A(2,﹣1)代入y= ![]() 可求出k=﹣2,從而得出一次函數和反比例函數的解析式;(2)令y=0,求得一次函數與x軸的交點坐標即為點C的坐標;(3)觀察函數圖象得到不等式0<x+m≤
可求出k=﹣2,從而得出一次函數和反比例函數的解析式;(2)令y=0,求得一次函數與x軸的交點坐標即為點C的坐標;(3)觀察函數圖象得到不等式0<x+m≤ ![]() 的解集為1<x≤2.
的解集為1<x≤2.


科目:初中數學 來源: 題型:
【題目】四邊形OBCD中的三個頂點在⊙O上,點A是⊙O上的一個動點(不與點B、C、D重合).若四邊形OBCD是平行四邊形時,那么∠OBA和∠ODA的數量關系是 . 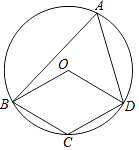
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】快車和慢車同時從甲、乙兩地出發開往乙地和甲地,勻速行駛,快車到達乙地后休息一個小時按原速返回,慢車在快車前一個小時到達甲地.如圖表示慢車行駛過程中離甲地的路程y(km)與出發時間x(h)的函數圖象,請結合圖中的信息,解答下列問題:

(1)甲、乙兩地的距離為 km,慢車的速度為 km/h,快車的速度為 km/h;
(2)在圖①中畫出快車離甲地的路程y(km)與出發時間x(h)的函數圖象(坐標軸標注相關數值);
(3)求出發多長時間,兩車相距150km.
查看答案和解析>>
科目:初中數學 來源: 題型:
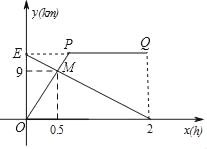
【題目】甲騎自行車從A地出發前往B地,同時乙步行從B地出發前往A地,如圖的折線OPQ和線段EF,分別表示甲、乙兩人與A地的距離y甲、y乙與他們所行時間x(h)之間的函數關系,且OP與EF相交于點M.
(1)求線段OP對應的y甲與x的函數關系式(不必注明自變量x的取值范圍);
(2)求y乙與x的函數關系式以及A,B兩地之間的距離;
(3)請從A,B兩題中任選一題作答,我選擇 題.
A.直接寫出經過多少小時,甲、乙兩人相距3km;
B.設甲、乙兩人的距離為s(km),直接寫出s與x的函數關系式,并注明x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】三角板是學習數學的重要工具,將一副三角板中的兩塊直角三角板的直角頂點![]() 按如圖方式疊放在一起,當
按如圖方式疊放在一起,當![]() 且點
且點![]() 在直線
在直線![]() 的上方時,解決下列問題:(友情提示:
的上方時,解決下列問題:(友情提示:![]() ,
,![]() ,
,![]() .
.

(1)①若![]() ,則
,則![]() 的度數為 ;
的度數為 ;
②若![]() ,則
,則![]() 的度數為 ;
的度數為 ;
(2)由(1)猜想![]() 與
與![]() 的數量關系,并說明理由.
的數量關系,并說明理由.
(3)這兩塊三角板是否存在一組邊互相平行?若存在,請直接寫出![]() 的角度所有可能的值(不必說明理由);若不存在,請說明理由.
的角度所有可能的值(不必說明理由);若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】解答題
(1)如圖1,在正方形ABCD中,點O是對角線AC的中點,點E是邊BC上一點,連接OE,過點O作OE的垂線交AB于點F.求證:OE=OF. 
(2)若將(1)中,“正方形ABCD”改為“矩形ABCD”,其他條件不變,如圖2,連接EF. ⅰ)求證:∠OEF=∠BAC.
ⅱ)試探究線段AF,EF,CE之間數量上滿足的關系,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】雅安地震,牽動著全國人民的心,地震后某中學舉行了愛心捐款活動,圖是根據該校九年級某班學生為雅安災區捐款情況繪制的不完整的條形統計圖和扇形統計圖.

(1)求該班學生總人數;
(2)補全條形統計圖;
(3)若該校九年級有800人,據此樣本,請你估計該校九年級學生共捐款多少元.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】先閱讀下列一段文字,再回答后面的問題.
已知在平面內兩點P1(x1,y1),P2(x2,y2),這兩點間的距離P1P2=![]() ,同時,當兩點所在的直線在坐標軸或平行于坐標軸或垂直于坐標軸時,兩點間距離公式可簡化為|x2﹣x1|或|y2﹣y1|.
,同時,當兩點所在的直線在坐標軸或平行于坐標軸或垂直于坐標軸時,兩點間距離公式可簡化為|x2﹣x1|或|y2﹣y1|.
(1)已知A(3,3),B(﹣2,﹣1),試求A,B兩點間的距離;
(2)已知A,B在平行于y軸的直線上,點A的縱坐標為7,點B的縱坐標為﹣2,試求A,B兩點間的距離;
(3)已知一個三角形各頂點坐標為A(0,5),B(﹣3,2),C(3,2),你能判斷此三角形的形狀嗎?說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com