Question

【題目】綜合題。
（1）問題發現：

如圖1，在Rt△ABC中，AB=AC=2，∠BAC=90°，點D為BC的中點，以CD為一邊作正方形CDEF，點E恰好與點A重合，則線段BE與AF的數量關系為
（2）拓展探究：

在（1）的條件下，如果正方形CDEF繞點C旋轉，連接BE、CE、AF，線段BE與AF的數量關系有無變化？請僅就圖2的情形給出證明；
（3）問題解決：
當正方形CDEF旋轉到B、E、F三點共線時候，直接寫出線段AF的長．

Answer 1

【答案】
（1）BE= AF；
（2）

解：無變化；理由如下：

如圖2，在Rt△ABC中，AB=AC=2，

∴∠ABC=∠ACB=45°，

∴sin∠ABC= ，

在正方形CDEF中，∠FEC= ∠FED=45°，

在Rt△CEF中，sin∠FEC= = ，

∴ ，

∵∠FCE=∠ACB=45°，

∴∠FCE﹣∠ACE=∠ACB﹣∠ACE，

∴∠FCA=∠ECB，

∴△ACF∽△BCE，

∴ = ，

∴BE= AF，

∴線段BE與AF的數量關系無變化；

（3）

解：當點E在線段AF上時，如圖2，

由（1）知，CF=EF=CD= ，

在Rt△BCF中，CF= ，BC=2 ，

根據勾股定理得，BF= ，

∴BE=BF﹣EF= ﹣ ，

由（2）知，BE= AF，

∴AF= ﹣1，

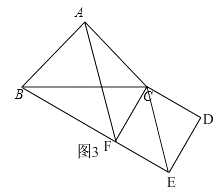
當點E在線段BF的延長線上時，如圖3，

在Rt△ABC中，AB=AC=2，

∴∠ABC=∠ACB=45°，

∴sin∠ABC═ ，

在正方形CDEF中，∠FEC= ∠FED=45°，

在Rt△CEF中，sin∠FEC= = ， ，

∵∠FCE=∠ACB=45°，

∴∠FCB+∠ACB=∠FCB+∠FCE，

∴∠FCA=∠ECB，

∴△ACF∽△BCE，

∴ = = ，

∴BE= AF，

由（1）知，CF=EF=CD= ，

在Rt△BCF中，CF= ，BC=2 ，

根據勾股定理得，BF= ，

∴BE=BF+EF= + ，

由（2）知，BE= AF，

∴AF= +1．

即當正方形CDEF旋轉到B、E、F三點共線時候，線段AF的長為 ﹣1或 +1

【解析】解：（1）在Rt△ABC中，AB=AC=2，
根據勾股定理得，BC= AB=2 ，
點D為BC的中點，
∴AD= BC= ，
∵四邊形CDEF是正方形，
∴AF=EF=AD= ，
∵BE=AB=2，
∴BE= AF，
所以答案是：BE= AF；
【考點精析】解答此題的關鍵在于理解勾股定理的概念的相關知識，掌握直角三角形兩直角邊a、b的平方和等于斜邊c的平方,即;a2+b2=c2，以及對正方形的性質的理解，了解正方形四個角都是直角，四條邊都相等；正方形的兩條對角線相等，并且互相垂直平分，每條對角線平分一組對角；正方形的一條對角線把正方形分成兩個全等的等腰直角三角形；正方形的對角線與邊的夾角是45o；正方形的兩條對角線把這個正方形分成四個全等的等腰直角三角形．