
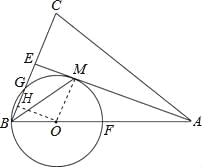
【題目】如圖,在△ABC中,AB=AC,AE是∠BAC的平分線,∠ABC的平分線 BM交AE于點M,點O在AB上,以點O為圓心,OB的長為半徑的圓經過點M,交BC于點G,交 AB于點F.
(1)求證:AE為⊙O的切線.
(2)當BC=8,AC=12時,求⊙O的半徑.
(3)在(2)的條件下,求線段BG的長.

【答案】(1)證明見解析;(2)3;(3)2.
【解析】試題分析:(1)連接OM.利用角平分線的性質和平行線的性質得到AE⊥OM后即可證得AE是⊙O的切線;
(2)設⊙O的半徑為R,根據OM∥BE,得到△OMA∽△BEA,利用平行線的性質得到![]() ,即可解得R=3,從而求得⊙O的半徑為3;
,即可解得R=3,從而求得⊙O的半徑為3;
(3)過點O作OH⊥BG于點H,則BG=2BH,根據∠OME=∠MEH=∠EHO=90°,得到四邊形OMEH是矩形,從而得到HE=OM=3和BH=1,證得結論BG=2BH=2.
試題解析:(1)證明:連接OM.
∵AC=AB,AE平分∠BAC,
∴AE⊥BC,CE=BE=![]() BC=4,
BC=4,
∵OB=OM,
∴∠OBM=∠OMB,
∵BM平分∠ABC,
∴∠OBM=∠CBM,
∴∠OMB=∠CBM,
∴OM∥BC
又∵AE⊥BC,
∴AE⊥OM,
∴AE是⊙O的切線;
(2)設⊙O的半徑為R,
∵OM∥BE,
∴△OMA∽△BEA,
∴![]() 即
即![]() ,
,
解得R=3,
∴⊙O的半徑為3;
(3)過點O作OH⊥BG于點H,則BG=2BH,
∵∠OME=∠MEH=∠EHO=90°,
∴四邊形OMEH是矩形,
∴HE=OM=3,
∴BH=1,
∴BG=2BH=2.


科目:初中數學 來源: 題型:
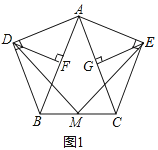
【題目】![]() 問題發現
問題發現
在等腰三角形ABC中,![]() ,分別以AB和AC為斜邊,向
,分別以AB和AC為斜邊,向![]() 的外側作等腰直角三角形,如圖1所示,其中
的外側作等腰直角三角形,如圖1所示,其中![]() 于點F,
于點F,![]() 于點G,M是BC的中點,連接MD和ME.
于點G,M是BC的中點,連接MD和ME.
填空:線段AF,AG,AB之間的數量關系是______;
線段MD,ME之間的數量關系是______.
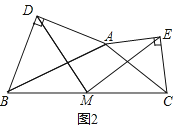
![]() 拓展探究
拓展探究
在任意三角形ABC中,分別以AB和AC為斜邊向![]() 的外側作等腰直角三角形,如圖2所示,M是BC的中點,連接MD和ME,則MD與ME具有怎樣的數量關系和位置關系?并說明理由;
的外側作等腰直角三角形,如圖2所示,M是BC的中點,連接MD和ME,則MD與ME具有怎樣的數量關系和位置關系?并說明理由;
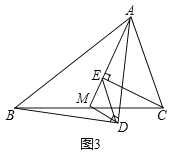
![]() 解決問題
解決問題
在任意三角形ABC中,分別以AB和AC為斜邊,向![]() 的內側作等腰直角三角形,如圖3所示,M是BC的中點,連接MD和ME,若
的內側作等腰直角三角形,如圖3所示,M是BC的中點,連接MD和ME,若![]() ,請直接寫出線段DE的長.
,請直接寫出線段DE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀材料:
學習了無理數后,某數學興趣小組開展了一次探究活動:估算![]() 的近似值.
的近似值.
小明的方法:
∵![]() <
<![]() <
<![]() ,
,
設![]() =3+k(0<k<1).
=3+k(0<k<1).
∴![]() .
.
∴13=9+6k+k2.
∴13≈9+6k.
解得 k≈![]() .
.
∴![]() ≈3+
≈3+![]() ≈3.67.
≈3.67.
問題:
(1)請你依照小明的方法,估算![]() 的近似值;
的近似值;
(2)請結合上述具體實例,概括出估算![]() 的公式:已知非負整數a、b、m,若a<
的公式:已知非負整數a、b、m,若a<![]() <a+1,且m=a2+b,則
<a+1,且m=a2+b,則![]() ≈ (用含a、b的代數式表示);
≈ (用含a、b的代數式表示);
(3)請用(2)中的結論估算![]() 的近似值.
的近似值.
查看答案和解析>>
科目:初中數學 來源: 題型:
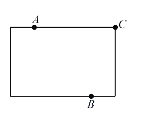
【題目】作圖題:
(1)為進一步打造“宜居北京”,某區擬在新竣工的矩形廣場的內部修建一個音樂噴泉,要求音樂噴泉 ![]() 到廣場的兩個入口
到廣場的兩個入口 ![]() ,
,![]() 的距離相等,且到廣場管理處
的距離相等,且到廣場管理處 ![]() 的距離等于
的距離等于 ![]() 和
和 ![]() 之間距離的一半,
之間距離的一半,![]() ,
,![]() ,
,![]() 的位置如圖所示.請在答題卷的原圖上利用尺規作圖作出音樂噴泉
的位置如圖所示.請在答題卷的原圖上利用尺規作圖作出音樂噴泉 ![]() 的位置.(要求:不寫已知、求作、作法和結論,保留作圖痕跡,必須用鉛筆作圖)
的位置.(要求:不寫已知、求作、作法和結論,保留作圖痕跡,必須用鉛筆作圖)
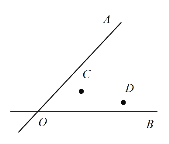
(2)如圖,兩條公路 ![]() 和
和 ![]() 相交于
相交于 ![]() 點,在
點,在 ![]() 的內部有工廠
的內部有工廠 ![]() 和
和 ![]() ,現要修建一個貨站
,現要修建一個貨站 ![]() ,使貨站
,使貨站 ![]() 到兩條公路
到兩條公路 ![]() ,
,![]() 的距離相等,且到兩工廠
的距離相等,且到兩工廠 ![]() ,
,![]() 的距離相等,用尺規作出貨站
的距離相等,用尺規作出貨站 ![]() 的位置.(要求:不寫作法,保留作圖痕跡,必須用鉛筆作圖)
的位置.(要求:不寫作法,保留作圖痕跡,必須用鉛筆作圖)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】現今“微信運動”被越來越多的人關注和喜愛,某興趣小組隨機調查了我市50名教師某日“微信運動”中的步數情況進行統計整理,繪制了如下的統計圖表(不完整):
步數 | 頻數 | 頻率 |
0≤x<4000 | 8 | a |
4000≤x<8000 | 15 | 0.3 |
8000≤x<12000 | 12 | b |
12000≤x<16000 | c | 0.2 |
16000≤x<20000 | 3 | 0.06 |
20000≤x<24000 | d | 0.04 |
請根據以上信息,解答下列問題:
(1)寫出a,b,c,d的值并補全頻數分布直方圖;
(2)本市約有37800名教師,用調查的樣本數據估計日行走步數超過12000步(包含12000步)的教師有多少名?
(3)若在50名被調查的教師中,選取日行走步數超過16000步(包含16000步的兩名教師與大家分享心得,求被選取的兩名教師恰好都在20000步(包含20000步)以上的概率.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在方格紙內將△ABC經過一次平移后得到△A′B′C′,圖中標出了點B的對應點B′.根據下列條件,利用網格點和三角尺畫圖:
(1)補全△A′B′C′
(2)畫出AC邊上的中線BD;
(3)畫出AC邊上的高線BE;
(4)求△ABD的面積 .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知四邊形ABCD中,AB=12厘米,BC=8厘米,CD=14厘米,∠B=∠C,點E為線段AB的中點.如果點P在線段BC上以3厘米秒的速度由B點向C點運動,同時,點Q在線段CD上由C點向D點運動.當點Q的運動速度為_____厘米/秒時,能夠使△BPE與以C、P、Q三點所構成的三角形全等.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com