
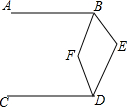
 如圖,AB∥CD,∠BED=110°,BF平分∠ABE,DF平分∠CDE,則∠BFD=125°.
如圖,AB∥CD,∠BED=110°,BF平分∠ABE,DF平分∠CDE,則∠BFD=125°. 分析 首先過點(diǎn)E作EM∥AB,過點(diǎn)F作FN∥AB,由AB∥CD,即可得EM∥AB∥CD∥FN,然后根據(jù)兩直線平行,同旁內(nèi)角互補(bǔ),由∠BED=110°,即可求得∠ABE+∠CDE=250°,又由BF平分∠ABE,DF平分∠CDE,根據(jù)角平分線的性質(zhì),即可求得∠ABF+∠CDF的度數(shù),又由兩只線平行,內(nèi)錯角相等,即可求得∠BFD的度數(shù).
解答 解:過點(diǎn)E作EM∥AB,過點(diǎn)F作FN∥AB,
∵AB∥CD,
∴EM∥AB∥CD∥FN,
∴∠ABE+∠BEM=180°,∠CDE+∠DEM=180°,
∴∠ABE+∠BED+∠CDE=360°,
∵∠BED=110°,
∴∠ABE+∠CDE=250°,
∵BF平分∠ABE,DF平分∠CDE,
∴∠ABF=$\frac{1}{2}$∠ABE,∠CDF=$\frac{1}{2}$∠CDE,
∴∠ABF+∠CDF=$\frac{1}{2}$(∠ABE+∠CDE)=125°,
∵∠DFN=∠CDF,∠BFN=∠ABF,
∴∠BFD=∠BFN+∠DFN=∠ABF+∠CDF=125°.
故答案為125°
點(diǎn)評 此題考查了平行線的性質(zhì)與角平分線的定義.此題難度適中,解題的關(guān)鍵是注意數(shù)形結(jié)合思想的應(yīng)用,注意輔助線的作法.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:填空題
 如圖,點(diǎn)E是正方形ABCD邊BC邊的延長線上一點(diǎn),且CE=$\frac{1}{2}$BC,BG⊥DE于點(diǎn)G,連接AG交CD于點(diǎn)F,BG交CD于點(diǎn)H,AB=$2\sqrt{5}$,則FG的長為$\frac{2\sqrt{2}}{3}$.
如圖,點(diǎn)E是正方形ABCD邊BC邊的延長線上一點(diǎn),且CE=$\frac{1}{2}$BC,BG⊥DE于點(diǎn)G,連接AG交CD于點(diǎn)F,BG交CD于點(diǎn)H,AB=$2\sqrt{5}$,則FG的長為$\frac{2\sqrt{2}}{3}$.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | x≥1 | B. | x≤1 | C. | x>1 | D. | x<1 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | x4+x4=2x8 | B. | x6÷x2=x3 | C. | (-x5)2=x10 | D. | xm•xn=xmn |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 60° | B. | 90° | C. | 120° | D. | 60°或120° |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com