
【題目】在平面直角坐標系中,規定:拋物線y=a(x﹣h)2+k的關聯直線為y=a(x﹣h)+k.
例如:拋物線y=2(x+1)2﹣3的關聯直線為y=2(x+1)﹣3,即y=2x﹣1.
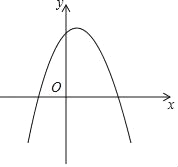
(1)如圖,對于拋物線y=﹣(x﹣1)2+3.
①該拋物線的頂點坐標為_____,關聯直線為_____,該拋物線與其關聯直線的交點坐標為_____和_____;
②點P是拋物線y=﹣(x﹣1)2+3上一點,過點P的直線PQ垂直于x軸,交拋物線y=﹣(x﹣1)2+3的關聯直線于點Q.設點P的橫坐標為m,線段PQ的長度為d(d>0),求當d隨m的增大而減小時,d與m之間的函數關系式,并寫出自變量m的取值范圍.
(2)頂點在第一象限的拋物線y=﹣a(x﹣1)2+4a與其關聯直線交于點A,B(點A在點B的左側),與x軸負半軸交于點C,直線AB與x軸交于點D,連結AC、BC.
①求△BCD的面積(用含a的代數式表示).
②當△ABC為鈍角三角形時,直接寫出a的取值范圍.
【答案】 (1,3) y=﹣x+4 (1,3) (2,2)
【解析】試題分析: ![]() ①直接寫出拋物線的頂點坐標,根據關聯直線的定義求出關聯直線的方程,聯立方程即可求出它們的交點坐標.
①直接寫出拋物線的頂點坐標,根據關聯直線的定義求出關聯直線的方程,聯立方程即可求出它們的交點坐標.
②設![]() 則
則![]() 因為d隨m的增大而減小,得出
因為d隨m的增大而減小,得出![]() 或
或![]() 分兩種情況進行討論.
分兩種情況進行討論.
![]() ①根據關聯直線的定義求出關聯直線的方程,聯立方程即可求出它們的交點
①根據關聯直線的定義求出關聯直線的方程,聯立方程即可求出它們的交點![]() 的坐標.求出
的坐標.求出![]() 兩點的坐標,根據三角形的面積公式進行求解即可.
兩點的坐標,根據三角形的面積公式進行求解即可.
②![]() 分兩種情況進行討論即可.
分兩種情況進行討論即可.
試題解析:(1)①拋物線的頂點坐標為![]() ,關聯直線為
,關聯直線為![]()
解方程組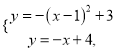 得
得![]() 或
或![]()
所以該拋物線與其關聯直線的交點坐標為![]() 和
和![]()
故答案為: ![]() ,
, ![]()
![]() 和
和![]()
②設![]() 則
則![]()
如圖1,
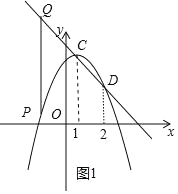
∵d隨m的增大而減小,
∴![]() 或
或![]()
當![]() 時,
時, ![]()
當![]() 時,
時, ![]()
當![]() ,d隨m的增大而減小,
,d隨m的增大而減小,
綜上所述,當![]() ,
, ![]()
![]() 時,
時, ![]()
(2)①拋物線![]() 的頂點坐標為:
的頂點坐標為: ![]() 在第一象限,則
在第一象限,則![]()
拋物線![]() 的關聯直線為
的關聯直線為![]()
解方程組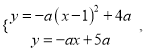 得
得![]() 或
或![]()
∴![]()
當![]() 時,
時, ![]() 解得
解得![]() 則
則![]()
當![]() 時,
時, ![]() 解得
解得![]() 則
則![]()
∴![]()
②![]()
當![]()
![]() 為鈍角,即
為鈍角,即![]() 解得
解得![]()
當![]()
![]() 為鈍角,即
為鈍角,即![]() 解得
解得![]()
綜上所述,a的取值范圍為![]() 或
或![]()


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】已知:數a,b,c 在數軸上的對應點如下圖所示,
(1)在數軸上表示﹣a;
(2)比較大小(填“<”或“>”或“=”):a+b 0,﹣3c 0,c﹣a 0;
(3)化簡|a+b|﹣|﹣3c|﹣|c﹣a|.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,甲、乙兩塊邊長為a米(a>1)的正方形田地,甲地修了兩條互相垂直的寬為1米的通道,乙地正中間修了邊長為1米的蓄水池,甲乙兩田地的剩余地方全部種植小麥,一年后收獲小麥m千克.(m>0)

(1)甲地的小麥種植面積為 平方米,乙地的小麥種植面積為 平方米;
(2)甲乙兩地小麥種植面積較小的是 地;
(3)若高的單位面積產量是低的單位面積產量的![]() 倍,求a的值.
倍,求a的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列方程變形中,正確的是( )
A.方程3x-2=2x+1,移項,得3x-2x=1-2
B.方程3-x=2-5(x-1),去括號,得3-x=2-5x-1;
C.方程-75x=76,方程兩邊同除以-75,得x=-![]()
D.方程![]() =1+
=1+![]() ,去分母,得2(2x-1)=6+3(x-3)
,去分母,得2(2x-1)=6+3(x-3)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,A、B兩點在數軸上對應的數分別為a,b,且點A在點B的左側;
![]()
(1)列方程解應用題:若AB的長度為115個單位長度,現有已知螞蟻P從A出發,以每秒3個單位長度的速度向右運動,5秒之后,另一只螞蟻Q從點B出發,以每秒2個單位長度的速度向左運動,求螞蟻Q出發多長時間后,兩只螞蟻在數軸上相遇?
(2)若∣a∣=20,a+b=100,ab<0,請求出a,b的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知正方形 ABCD 的邊長為 1,以頂點 A、B 為圓心,1 為半徑的兩弧交于點 E, 以頂點 C、D 為圓心,1 為半徑的兩弧交于點 F,則 EF 的長為 ( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】由若干個邊長為1的小正方形組成的網格,小正方形的頂點叫做格點,以格點為頂點的多邊形叫格點多邊形.設格點多邊形的面積為S,它各邊上格點的個數和為x.
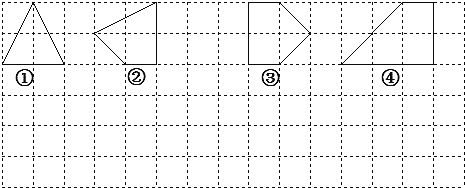
(1)上圖中的格點多邊形,其內部都只有一個格點,它們的面積(S)與各邊上格點的個數和(x)的對應關系如下表,請寫出S與x之間的關系式.答:S=_________.
多邊形的序號 | ① | ② | ③ | ④ | … |
多邊形的面積S | 2 | 2.5 | 3 | 4 | … |
各邊上格點的個數和x | 4 | 5 | 6 | 8 | … |
(2)請再畫出三個邊數分別為3、4、5的格點多邊形,使這些多邊形內部都是有且只有2個格點.可得此類多邊形的面積(S)與它各邊上格點的個數和(x)之間的關系式是:S=________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,矩形ABCD中,AE平分![]() 交BC于E,
交BC于E,![]() ,則下面的結論:①
,則下面的結論:①![]() 是等邊三角形;②
是等邊三角形;②![]() ;③
;③![]() ;④
;④![]() ,其中正確結論有( )
,其中正確結論有( )
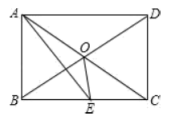
A. 1個B. 2個C. 3個D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知反比例函數y=![]() 的圖象與一次函數y=ax+b的圖象交于點A(1,4)和點B(m,﹣2),
的圖象與一次函數y=ax+b的圖象交于點A(1,4)和點B(m,﹣2),
(1)求這兩個函數的關系式;
(2)觀察圖象,寫出使得![]() >ax+b成立的自變量x的取值范圍;
>ax+b成立的自變量x的取值范圍;
(3)過點A作AC⊥x軸,垂足為C,在平面內有點D,使得以A,O,C,D四點為頂點的四邊形為平行四邊形,直接寫出符合條件的所有D點的坐標.
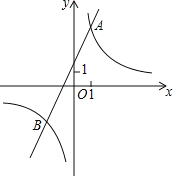
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com