
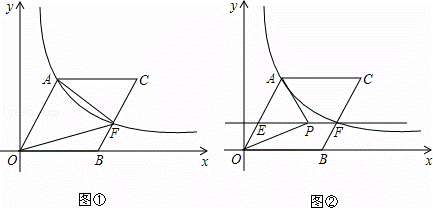
如圖①,O為坐標原點,點B在x軸的正半軸上,四邊形OACB是平行四邊形,sin∠AOB=4/5,反比例函數y= k(k>0)在第一象限內的圖象經過點A,與BC交于點F.
(1)若OA=10,求反比例函數解析式;
(2)若點F為BC的中點,且△AOF的面積S=12,求OA的長和點C的坐標;
(3)在(2)中的條件下,過點F作EF∥OB,交OA于點E(如圖②),點P為直線EF上的一個動點,連接PA,PO.是否存在這樣的點P,使以P、O、A為頂點的三角形是直角三角形?若存在,請直接寫出所有點P的坐標;若不存在,請說明理由.
|
|


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
將軍家俱市場現有大批如圖所示的邊角余料(單位:cm)城西中學數學興趣小組決定將其加工成等腰三角形,且方案如下:
(1)三角形中至少有一邊長為10 cm;
(2)三角形中至少有一邊上的高為8 cm
請在備用圖上畫出出分割線,并求出相應圖形面積
 |  |  | |||
查看答案和解析>>
科目:初中數學 來源: 題型:
設a,b是任意兩個不等實數,我們規定:滿足不等式a≤x≤b的實數x的所有取值的全體叫做閉區間,表示為{a,b},對于一個函數,如果它的自變量x與函數值y滿足:當m≤x≤n時,有m≤y≤n,我們就稱此函數是閉區間{m,n}上的“閉函數”.
(1)反比列函數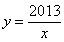 是閉區間{1,2013}上的“閉函數”嗎?請判斷并說明理由;
是閉區間{1,2013}上的“閉函數”嗎?請判斷并說明理由;
(2)若一次函數y=kx+b(k≠0)是閉區間{m,n}上的“閉函數”,求此函數的解析式:
查看答案和解析>>
科目:初中數學 來源: 題型:
一個立方體展開后各面上分別標有數字1,2,3,4, 6,8,其表面展開圖如圖所示,拋擲這個立方體,則朝上一面的數字恰好等于朝下一面數字的2倍的概率是( )
A、 B、
B、 C、
C、 D、
D、

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com