
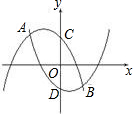
 如圖,拋物線F1:y1=-x2-x+1與拋物線F2:y2=x2-x-1相交于A、B兩點,拋物線F1與拋物線F2分別交y軸于點C、點D
如圖,拋物線F1:y1=-x2-x+1與拋物線F2:y2=x2-x-1相交于A、B兩點,拋物線F1與拋物線F2分別交y軸于點C、點D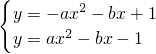 ,
,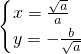 ,
,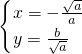 ;
; ,
, ),B(
),B( ,-
,- );
); CD×|xB-xA|=
CD×|xB-xA|= ×2×
×2×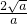 =
=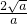 .
. =
= =0,
=0, ,-
,- ),B(
),B( ,
, ),由此可發現C、D以及A、B都關于原點O對稱,那么AB、CD互相平分,所有四邊形ACBD是平行四邊形;那么它的面積可由CD與A、B橫坐標差的絕對值的積的一半求得;根據這些結論即可得到(1)題的填空答案.
),由此可發現C、D以及A、B都關于原點O對稱,那么AB、CD互相平分,所有四邊形ACBD是平行四邊形;那么它的面積可由CD與A、B橫坐標差的絕對值的積的一半求得;根據這些結論即可得到(1)題的填空答案.

 小學課時特訓系列答案
小學課時特訓系列答案科目:初中數學 來源: 題型:
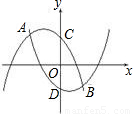
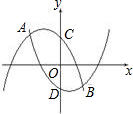 如圖,拋物線F1:y1=-x2-x+1與拋物線F2:y2=x2-x-1相交于A、B兩點,拋物線F1與拋物線F2分別交y軸于點C、點D
如圖,拋物線F1:y1=-x2-x+1與拋物線F2:y2=x2-x-1相交于A、B兩點,拋物線F1與拋物線F2分別交y軸于點C、點D查看答案和解析>>
科目:初中數學 來源: 題型:

| 1 |
| 3 |
| 2 |
| 3 |
| 7 |
| 3 |
| 3 |
查看答案和解析>>
科目:初中數學 來源:2011年天津市河東區中考數學一模試卷(解析版) 題型:解答題

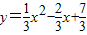 經過變換滿足AC=2
經過變換滿足AC=2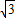 ,點P是直線AC上的動點,求點P到點D的距離與到直線AD的距離之和的最小值.
,點P是直線AC上的動點,求點P到點D的距離與到直線AD的距離之和的最小值.查看答案和解析>>
科目:初中數學 來源:2010年中考數學模擬卷(11)(解析版) 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com