Question

如果P是邊長為4的等邊三角形內任意一點，那么點P到三角形三邊距離之和為    ．

Answer 1

【答案】分析：作出圖形，根據等邊三角形的性質求出高AH的長，再根據三角形的面積公式求出點P到三邊的距離之和等于高線的長度，從而得解．
解答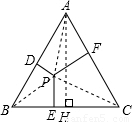：解：如圖，∵等邊三角形的邊長為4，
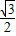
∴高線AH=4×=2，
S_△ABC=BC•AH=AB•PD+BC•PE+AC•PF，
∴×4•AH=×4•PD+×4•PE+×4•PF，
∴PD+PE+PF=AH=2，
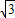
即點P到三角形三邊距離之和為2．
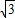
故答案為：2．
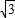
點評：本題考查了等邊三角形的性質，根據三角形的面積求點P到三邊的距離之和等于等邊三角形的高是解題的關鍵，作出圖形更形象直觀．