
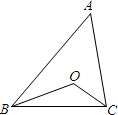
 如圖,△ABC中,下面說法正確的個數是個.
如圖,△ABC中,下面說法正確的個數是個. (∠ABC+∠ACB)進而求出即可;
(∠ABC+∠ACB)進而求出即可; (∠ABC+∠ACB)=180°-
(∠ABC+∠ACB)=180°- (180°-∠A)=115°,故此選項正確;
(180°-∠A)=115°,故此選項正確;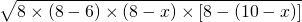 =4
=4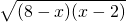 ≤4×
≤4×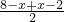 =12,
=12, x×16=12,
x×16=12,

 周周清檢測系列答案
周周清檢測系列答案 輕巧奪冠周測月考直通高考系列答案
輕巧奪冠周測月考直通高考系列答案科目:初中數學 來源: 題型:
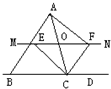 25、如圖,△ABC中,點O是AC邊上的一個動點,過點O作直線MN∥BC,設MN交∠BCA的平分線于點E,交∠BCA的外角平分線于點F.
25、如圖,△ABC中,點O是AC邊上的一個動點,過點O作直線MN∥BC,設MN交∠BCA的平分線于點E,交∠BCA的外角平分線于點F.查看答案和解析>>
科目:初中數學 來源: 題型:

| 連接個數 | ||||||
| 出現三角形個數 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 27、如圖,△ABC中,點O在邊AB上,過點O作BC的平行線交∠ABC的平分線于點D,過點B作BE⊥BD,交直線OD于點E.
27、如圖,△ABC中,點O在邊AB上,過點O作BC的平行線交∠ABC的平分線于點D,過點B作BE⊥BD,交直線OD于點E.查看答案和解析>>
科目:初中數學 來源: 題型:
 (2013•莒南縣一模)如圖,△ABC中,AD是邊BC上的中線,過點A作AE∥BC,過點D作DE∥AB,DE與AC、AE分別交于點O、點E,連接EC
(2013•莒南縣一模)如圖,△ABC中,AD是邊BC上的中線,過點A作AE∥BC,過點D作DE∥AB,DE與AC、AE分別交于點O、點E,連接EC查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,△ABC中,DE∥AC交AB于E,DF∥AB交AC于F,AD是△ABC的角平分線,那么四邊形AEDF的形狀是
如圖,△ABC中,DE∥AC交AB于E,DF∥AB交AC于F,AD是△ABC的角平分線,那么四邊形AEDF的形狀是查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com