

分析 (1)①利用圓的“完美點”的定義直接判斷即可得出結論;
②先確定出滿足圓的“完美點”的OP的長度,然后分情況討論計算即可得出結論;
(2)先判斷出圓的“完美點”的軌跡,然后確定出取極值時⊙C與y軸的位置關系即可得出結論.
解答 解:(1)①∵點M($\frac{3}{2}$,0),
∴設⊙O與x軸的交點為A,B,
∵⊙O的半徑為2,
∴取A(-2,0),B(2,0),
∴|MA-MB|=|($\frac{3}{2}$+2)-($\frac{3}{2}$-2)|=4≠2,
∴點M不是⊙O的“完美點”,
同理:點N,T是⊙O的“完美點”.
故答案為N,T;
②如圖1,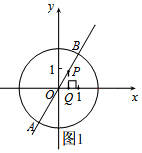 根據題意,|PA-PB|=2,
根據題意,|PA-PB|=2,
∴|OP+2-(2-OP)|=2,
∴OP=1.
若點P在第一象限內,作PQ⊥x軸于點Q,
∵點P在直線$y=\sqrt{3}x$上,OP=1,
∴OQ=$\frac{1}{2}$,PQ=$\frac{{\sqrt{3}}}{2}$.
∴P($\frac{1}{2}$,$\frac{{\sqrt{3}}}{2}$).
若點P在第三象限內,根據對稱性可知其坐標為(-$\frac{1}{2}$,-$\frac{{\sqrt{3}}}{2}$).
綜上所述,PO的長為1,點P的坐標為($\frac{1}{2}$,$\frac{{\sqrt{3}}}{2}$)或(-$\frac{1}{2}$,-$\frac{{\sqrt{3}}}{2}$).
(2)對于⊙C的任意一個“完美點”P都有|PA-PB|=2,
∴|CP+2-(2-CP)|=2.
∴CP=1.
∴對于任意的點P,滿足CP=1,都有|CP+2-(2-CP)|=2,
∴|PA-PB|=2,故此時點P為⊙C的“完美點”.
因此,⊙C的“完美點”是以點C為圓心,1為半徑的圓.
設直線$y=\sqrt{3}x+1$與y軸交于點D,如圖2,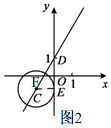
當⊙C移動到與y軸相切且切點在點D的下方時,t的值最小.
設切點為E,連接CE,
∵⊙C的圓心在直線y=$\sqrt{3}$x+1上,
∴此直線和y軸,x軸的交點D(0,1),F(-$\frac{\sqrt{3}}{3}$,0),
∴OF=$\frac{\sqrt{3}}{3}$,OD=1,
∵CE∥OF,
∴△DOF∽△DEC,
∴$\frac{OD}{DE}=\frac{OF}{CE}$,
∴$\frac{1}{DE}=\frac{\frac{\sqrt{3}}{3}}{2}$,
∴DE=2$\sqrt{3}$.
∴OE=2$\sqrt{3}$-1,
t的最小值為1-2$\sqrt{3}$.
當⊙C移動到與y軸相切且切點在點D的上方時,t的值最大.
同理可得t的最大值為1+2$\sqrt{3}$.
綜上所述,t的取值范圍為1-2$\sqrt{3}$≤t≤1+2$\sqrt{3}$.
點評 此題是圓的綜合題,主要考查了新定義,相似三角形的性質和判定,直線和圓的位置關系,解本題的關鍵是理解新定義的基礎上,會用新定義,是一道比中等難度的中考常考題.


科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,三角形紙片ABC中,∠BCA=90°,在AC上取一點E,以BE為折痕進行翻折,使AB的一部分與BC重合,A與BC延長線上的點D重合,若∠A=30°,AC=6,則,DE的長度為( )
如圖,三角形紙片ABC中,∠BCA=90°,在AC上取一點E,以BE為折痕進行翻折,使AB的一部分與BC重合,A與BC延長線上的點D重合,若∠A=30°,AC=6,則,DE的長度為( )| A. | 6 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 平面直角坐標系xOy中,對稱軸平行于y軸的拋物線過點A(1,0)、B(3,0)和C(4,6);
平面直角坐標系xOy中,對稱軸平行于y軸的拋物線過點A(1,0)、B(3,0)和C(4,6);查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com