Question

現計劃把甲種貨物1240噸和乙種貨物880噸用一列貨車運往某地，已知這列貨車掛有A、B兩種不同規格的貨車廂共40節，使用A型車廂每節費用為0.6萬元，使用B型車廂每節費用為0.8萬元．

1.設運送這批貨物的總費用為y萬元，這列貨車掛A型車廂x節，試寫出y與x之間的函數關系式；

2.如果每節A型車廂最多可裝甲種貨物35噸和乙種貨物15噸，每節B型車廂最多可裝甲種貨物25噸和乙種貨物35噸，裝貨時按此要求安排A、B兩種車廂的節數，那么共有哪幾種安排車廂的方案？

3.在上述方案中，哪個方案運費最省？最少運費為多少元？

 

Answer 1

【答案】

 

1.設用A型車廂x節，則用B型車廂(40－x)節，總運費為y萬元 ．-------1分

依題意，得  y＝0.6 x＋0.8(40－x)      --------------------------------3分

             ＝－0.2 x＋32    ----------------------------------------4分

2.依題意，得

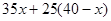≥1240，

≥880．       ---------------------------6分

化簡，得   10 x≥240，     x≥24，  

            520≥20 x；      x≤26．

∴  24≤x≤26．                           --------------------------7分

∵  x取整數，故A型車廂可用24節或25節或26節．相應有三種裝車方案：①24節A型車廂和16節B型車廂；②25節A型車廂和15節B型車廂；③26節A型車廂和14節B型車廂．     ----------------------------------------------------------8分

3.由函數y＝－0. 2 x＋32知，x越大，y越少，

故當x＝26時，運費最省．----------------------------------------------10分

這時 y＝－0.2×26＋32＝26.8(萬元)                       --------------11分

答：安排A型車廂26節、B型車廂14節運費最省．最小運費為26.8萬元．----12分　　  　　　　　                                      

（注：若直接算出三種方案的運費來比較，得出正確的最少運費亦給滿分。）

【解析】（1）總費用=0.6×A型車廂節數+0.8×B型車廂節數．

（2）應分別表示出兩類車廂能裝載的甲乙兩種貨物的質量．35×A型車廂節數+25×B型車廂節數≥1240；15×A型車廂節數+35×B型車廂節數≥880．

（3）應結合（1）的函數，（2）的自變量的取值來解決