
 已知:兩個等腰直角三角形(△ACB和△BED)邊長分別為a和b(a<b)如圖放置在一起,連接AD,
已知:兩個等腰直角三角形(△ACB和△BED)邊長分別為a和b(a<b)如圖放置在一起,連接AD,| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
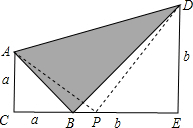 解:(1)如右圖所示,
解:(1)如右圖所示,| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


 發(fā)散思維新課堂系列答案
發(fā)散思維新課堂系列答案科目:初中數(shù)學 來源: 題型:
| 9 | 8 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
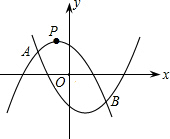
 ,且與拋物線y2=ax2-ax-1相交于A,B兩點.設A,B兩點的橫坐標分別記為xA,xB,若在x軸上有一動點Q(x,0),且xA≤x≤xB,過q作一條垂直于x軸的直線,與兩條拋物線分別交于C,D兩點,試問當x為何值時,線段CD有最大值,其最大值為多少?
,且與拋物線y2=ax2-ax-1相交于A,B兩點.設A,B兩點的橫坐標分別記為xA,xB,若在x軸上有一動點Q(x,0),且xA≤x≤xB,過q作一條垂直于x軸的直線,與兩條拋物線分別交于C,D兩點,試問當x為何值時,線段CD有最大值,其最大值為多少?
查看答案和解析>>
科目:初中數(shù)學 來源:2011年河北省石家莊市裕華區(qū)中考數(shù)學二模試卷(解析版) 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com