已知正方形的邊長為x,面積為y
(1)寫出y與x的函數關系式;
(2)當面積為25時,正方形的邊長是多少?
(3)畫出此函數的圖象.
【答案】
分析:(1)由正方形的邊長為x,面積為y,根據正方形面積的求解方法,即可求得y與x的函數關系式;
(2)當面積為25時,即y=25,將其代入函數解析式,即可求得x的值,即正方形的邊長;
(3)因為是實際問題,所以畫出二次函數y=x
2在第一象限的圖象即可.
解答: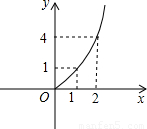
解:(1)∵正方形的邊長為x,面積為y,
∴y=x
2,
∴y與x的函數關系式為y=x
2;
(2)∵面積為25時,即y=25,
∴x
2=25,
解得:x=5或x=-5(舍去),
∴正方形的邊長是5;
(3)如圖:
點評:此題考查了二次函數的實際應用問題與正方形的面積的求解方法.此題難度不大,解題的關鍵是理解題意,根據題意求得二次函數解析式,再利用函數性質求解.

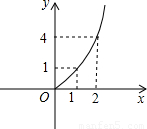 解:(1)∵正方形的邊長為x,面積為y,
解:(1)∵正方形的邊長為x,面積為y,
