如圖,已知A,B兩點的坐標分別為(2,0),(0,2),⊙C的圓心坐標為(-1,0),半徑為1.若D是⊙C上的一個動點,線段DA與y軸交于點E ,則△ABE面積的最小值是 _____
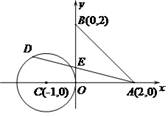
根據(jù)三角形的面積公式,△ABE底邊BE上的高AO不變,BE越小,則面積越小,可以判斷當AD與⊙C相切時,BE的值最小,根據(jù)勾股定理求出AD的值,然后根據(jù)相似三角形對應(yīng)邊成比例列式求出OE的長度,代入三角形的面積公式進行計算即可求解.
解:如圖所示,當AD與⊙C相切時,點BE最短,此時△ABE面積的最小,

∵A(2,0),C(-1,0),⊙C半徑為1,
∴AO=2,AC=2+1=3,CD=1,
在Rt△ACD中,AD=
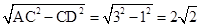
,
∵CD⊥AD,
∴∠D=90°,
∴∠D=∠AOE,
在△AOE與△ADC中,

,
∴△AOE∽△ADC,
∴
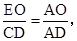
即
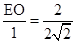
,
解得EO=
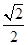
,
∵點B(0,2),
∴OB=2,
∴BE=OB-OE=2-
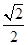
,
∴△ABE面積的最小值=
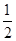
×BE×AO=
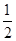
(2-
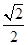
)×2=2-
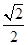
.
故答案為:2-
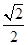
.
練習冊系列答案
相關(guān)習題
科目:初中數(shù)學
來源:不詳
題型:填空題
若⊙O1和⊙O2相交于點A、B,且AB=24,⊙O1的半徑為13,⊙O2的半徑15,則O1O2的長為__________或__________.(有兩解)
查看答案和解析>>
科目:初中數(shù)學
來源:不詳
題型:解答題
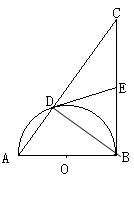
如圖,以
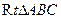
的直角邊
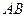
為直徑的半圓
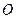
,與斜邊
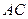
交于
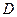
,
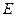
是
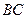
邊上的中點. 連結(jié)
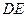
,
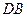
. 試問
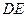
與半圓
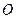
相切嗎?若相切,請給出證明;若不相切,請說明理由.
查看答案和解析>>
科目:初中數(shù)學
來源:不詳
題型:填空題
已知⊙O1和⊙O2的半徑分別為1cm和4cm,且它們內(nèi)切,則圓心距O1O2等于______________cm.
查看答案和解析>>
科目:初中數(shù)學
來源:不詳
題型:填空題
已知正六邊形的半徑為
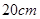
,則它的外接圓與內(nèi)切圓組成的圓環(huán)的面積是_______
查看答案和解析>>
科目:初中數(shù)學
來源:不詳
題型:解答題
如圖,⊙I為△ABC的內(nèi)切圓,AB=9,BC=8,CA=10,點D,E分別為AB,AC上的點,且DE為⊙I的切線,
求△ADE的周長。
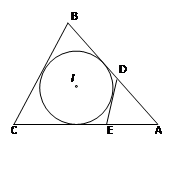
查看答案和解析>>
科目:初中數(shù)學
來源:不詳
題型:填空題
如圖,在⊙
O中,弦
AB=1.8cm,圓周角∠
ACB=30°,則⊙
O的直徑為__________cm.

查看答案和解析>>
科目:初中數(shù)學
來源:不詳
題型:解答題
(12分)如圖,AB是⊙O的一條弦,OD⊥AB,垂足為C,交⊙O于點D,點E在⊙O上.
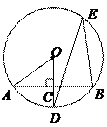
小題1:(1)若
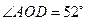
,求
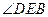
的度數(shù);
小題2:(2)若
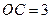
,
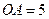
,求

的長.
查看答案和解析>>


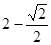

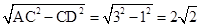 ,
, ,
,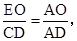
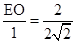 ,
,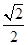 ,
,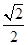 ,
,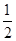 ×BE×AO=
×BE×AO=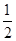 (2-
(2-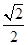 )×2=2-
)×2=2-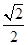 .
.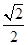 .
.

 名校課堂系列答案
名校課堂系列答案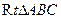 的直角邊
的直角邊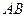 為直徑的半圓
為直徑的半圓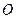 ,與斜邊
,與斜邊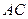 交于
交于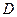 ,
,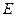 是
是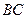 邊上的中點. 連結(jié)
邊上的中點. 連結(jié)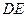 ,
,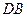 . 試問
. 試問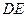 與半圓
與半圓 相切嗎?若相切,請給出證明;若不相切,請說明理由.
相切嗎?若相切,請給出證明;若不相切,請說明理由.
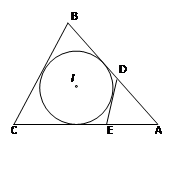
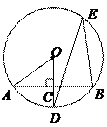
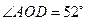 ,求
,求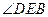 的度數(shù);
的度數(shù);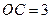 ,
,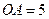 ,求
,求 的長.
的長.