
【題目】已知:在△ABC中,AB=AC,點D是AB上一點,以BD為直徑的⊙0與AC邊相切于點E,交BC于點F,FG⊥AC于點G.
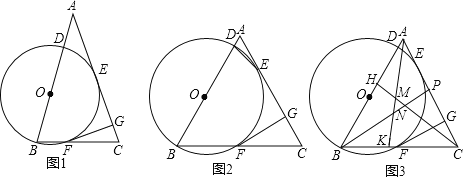
(1)如圖l,求證:GE=GF;
(2)如圖2,連接DE,∠GFC=2∠AED,求證:△ABC為等邊三角形;
(3)如圖3,在(2)的條件下,點H、K、P分別在AB、BC、AC上,AK、BP分別交CH于點M、N,AH=BK,∠PNC﹣![]() ∠BAK=60°,CN=6,CM=4
∠BAK=60°,CN=6,CM=4![]() ,求BC的長.
,求BC的長.
【答案】(1)見解析;(2)見解析;(3)BC=10.
【解析】
(1)由切線的定義得到直角條件,由半徑相等可證OFGE為正方形;
(2)由圓周角定理可得直角條件,由2倍角關系可得60°條件,從而證明等邊三角形;
(3)結合(2)的結論和條件中角的關系,需要設置角參數,標識圖形從而發現BC=BR,用勾股定理建立方程關系,求解方程即可.
解:(1)如圖1,連接OE和OF
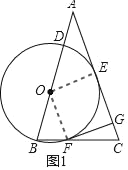
∵AC是⊙O的切線
∴OE⊥AC,
∴∠OEG=90°
∵FG⊥AC,
∴∠FGE=90°
∵AB=AC,
∴∠ABC=∠ACB
∵OB=OF,
∴∠OBF=∠OFB
∴∠OFB=∠ACB,
∴OF∥AC
∴∠OFG+∠FGE=180°,
∴∠OFG=90°
∴∠OFG=∠FGE=∠OEG=90°
∴四邊形OFGE為矩形
∵OF=OE,
∴四邊形OFGE為正方形
∴GE=GF
(2)如圖2,連接OE,BE
∵BD是⊙O的直徑,
∴∠BED=90°
∴∠OED+∠OEB=90°
∵∠OEG=90°,
∴∠AED+∠OED=90°
∵∠OEG=90°,
∴∠AED+∠OED=90°
∴∠OEB=∠AED
∵OB=OE,
∴∠OBE=∠OEB
∴∠OBE=∠AED
∴∠AOE=2∠OEB=2∠AED
∵∠GFC=2∠AED
∴∠AOE=∠GFC
∵∠C+∠GFC=90°,∠A+∠AOE=90°
∴∠C=∠A
∴BA=BC,
∵AB=AC
∴AB=AC=BC
∴△ABC為等邊三角形
(3)∵△ABC為等邊三角形
∴∠CAH=∠ABK=60°
∵AH=BK,AC=AB,
∴△CAH≌△ABK(SAS)
∴∠ACH=∠BAK
∵∠KMC=∠KAC+∠ACM
∴∠KMC=∠KAC+∠BAK=60°
過點C作CQ⊥AK,垂足為Q,過點B作BT⊥CH,垂足為T
∴∠AQC=∠CTB=90°
∵∠QAC=∠BAC﹣∠BAK=60°,∠TCB=∠ACB﹣∠ACH=60°﹣∠ACH
∴∠QAC=∠TCB,
∵AC=BC
∴△AQC≌△CTB(AAS)
∴QC=BT
在Rt△MQC中,
∵CM=4![]() ,∠QMC=60°,sin∠QMC=
,∠QMC=60°,sin∠QMC=![]()
∴QC=6
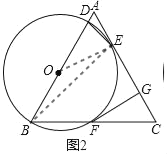
設∠BAK=2α=∠ACH
∵∠PNC﹣![]() ∠BAK=60°,
∠BAK=60°,
∴∠PNC=60°+α=∠BNH
∴∠BCH=∠ACB﹣∠ACH=60°﹣2α
延長NH到點R,使RT=TN,連接BR
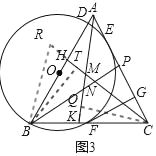
∴BT使RN的垂直平分線
∴BR=BN
∴∠BNR=∠BRN=60°+α
∴∠CBR=180°﹣∠BCR﹣∠CRB=60°+α
∴∠CBR=∠CRB=60°+α
∴BC=RC
設TN=RT=a,
∵CN=6
∴CT=a+6,CR=CB=2a+6
∵CQ=BT=6
在Rt△BTC中
BT2+TC2=BC2
∴62+(a+6)2=(2a+6)2
∴a1=﹣6(舍),a2=2
∴TN=2
∴BC=10


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
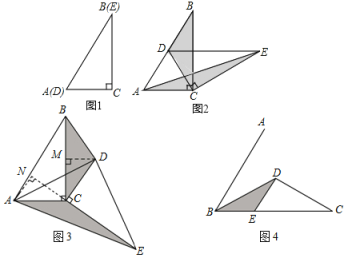
【題目】如圖1,將兩個完全相同的三角形紙片![]() 和
和![]() 重合放置,其中
重合放置,其中![]() ,
,![]() .
.
(1)操作發現
如圖2,固定![]() ,使
,使![]() 繞點
繞點![]() 旋轉,當點
旋轉,當點![]() 恰好落在
恰好落在![]() 邊上時,填空:
邊上時,填空:
①線段![]() 與
與![]() 的位置關系是______;
的位置關系是______;
②設![]() 的面積為
的面積為![]() ,
,![]() 的面積為
的面積為![]() ,則
,則![]() 與
與![]() 的數量關系是______
的數量關系是______
(2)猜想論證
當![]() 繞點
繞點![]() 旋轉到如圖3所示的位置時,小明猜想1.中
旋轉到如圖3所示的位置時,小明猜想1.中![]() 與
與![]() 的數量關系仍然成立,并嘗試分別作出了
的數量關系仍然成立,并嘗試分別作出了![]() 和
和![]() 中
中![]() 、
、![]() 邊上的高,請你證明小明的猜想.
邊上的高,請你證明小明的猜想.
(3)拓展探究
已知∠ABC=60°,點![]() 是角平分線上一點,
是角平分線上一點,![]() ,
,![]() 交
交![]() 于點
于點![]() (如圖4).若在射線
(如圖4).若在射線![]() 上存在點
上存在點![]() ,使
,使![]() ,請求出相應的
,請求出相應的![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,□ABCD的對角線AC,BD交于點O,CE平分∠BCD交AB于點E,交BD于點F,且∠ABC=60°,AB=2BC,連接OE.下列結論:①EO⊥AC;②S△AOD=4S△OCF;③AC:BD=![]() :7;④FB2=OFDF.其中正確的是( )
:7;④FB2=OFDF.其中正確的是( )
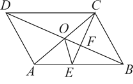
A.①②④B.①③④C.②③④D.①③
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】[知識回顧]
七年級學習代數式求值時,遇到這樣一類題 “代數式![]() 的值與
的值與![]() 的取值無關,求
的取值無關,求![]() 的值”,通常的解題方法是:把
的值”,通常的解題方法是:把![]() 看作字母,
看作字母,![]() 看作系數合并同類項,因為代數式的值與
看作系數合并同類項,因為代數式的值與![]() 的取值無關,所以含
的取值無關,所以含![]() 項的系數為
項的系數為![]() ,即原式
,即原式![]() ,所以
,所以![]() ,則
,則![]() .
.
[理解應用]
![]() 若關于
若關于![]() 的多項式
的多項式![]() 的值與
的值與![]() 的取值無關,試求
的取值無關,試求![]() 的值:
的值:
![]() 若一次函數
若一次函數![]() 的圖像經過某個定點,則該定點坐標為 ;
的圖像經過某個定點,則該定點坐標為 ;
[能力提升]
![]() 張如圖1的小長方形,長為
張如圖1的小長方形,長為![]() ,寬為
,寬為![]() ,按照圖2方式不重疊地放在大矩形
,按照圖2方式不重疊地放在大矩形![]() 內,大矩形中未被覆蓋的兩個部分(圖中陰影部分) ,設右上角的面積為
內,大矩形中未被覆蓋的兩個部分(圖中陰影部分) ,設右上角的面積為![]() ,左下角的面積為
,左下角的面積為![]() ,當
,當![]() 的長變化時,
的長變化時,![]() 的值始終保持不變,求
的值始終保持不變,求![]() 與
與![]() 的等量關系.
的等量關系.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,點E是BC上一點,連接AE,點F是AE上一點,連接FC,若∠BAE=∠EFC,CF=CD,AB:BC=3:2,AF=4,則FC的長為_____.
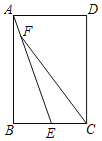
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】初一(1)班針對“你最喜愛的課外活動項目”對全班學生進行調查(每名學生分別選一個活動項目),并根據調查結果列出統計表,繪制成扇形統計圖.

根據以上信息解決下列問題:
(1)![]() ,
,![]() ;
;
(2)扇形統計圖中機器人項目所對應扇形的圓心角度數為 ![]() ;
;
(3)從選航模項目的![]() 名學生中隨機選取
名學生中隨機選取![]() 名學生參加學校航模興趣小組訓練,請用列舉法(畫樹狀圖或列表)求所選取的
名學生參加學校航模興趣小組訓練,請用列舉法(畫樹狀圖或列表)求所選取的![]() 名學生中恰好有
名學生中恰好有![]() 名男生、
名男生、![]() 名女生的概率.
名女生的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD中,AD∥BC,AB=CD,BD平分∠ABC,BD⊥DC.
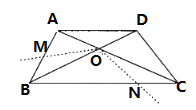
(1)求出sin∠DBC的值;
(2)若AD=2,把∠BOC繞點O順時針旋轉![]() (
(![]() ),交AB于點M,交BC于點N(如圖),求證:四邊形OMBN的面積為一個定值,并求出這個定值.
),交AB于點M,交BC于點N(如圖),求證:四邊形OMBN的面積為一個定值,并求出這個定值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在新中國成立70周年之際,某校開展了“校園文化藝術”活動,活動項目有:書法、繪畫、聲樂和器樂,要求全校學生人人參加,并且每人只能參加其中一項活動,政教處在該校學生中隨機抽取了100名學生進行調查和統計,并繪制了如下兩幅不完整的統計圖,請結合圖中相關數據解答下列問題:
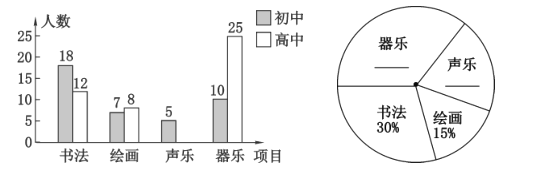
(1)請補全條形統計圖和扇形統計圖;
(2)該校初中學生中,參加“書法”項目的學生所占的百分比是多少?
(3)若該校共有1500人,請估計其中參加“器樂”項目的高中學生有多少人?
(4)經政教處對所有參加“繪畫”項目的作品進行評比,共選出2名初中學生和2名高中學生的最佳作品,學校決定從這4名學生中隨機抽取2人作為學生會“繪畫社團”的團生,那么正好抽到一名初中學生和一名高中學生的概率是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校九年級(1)班全體學生2018年初中畢業體育學業考試成績統計表如下:
成績/分 | 45 | 49 | 52 | 54 | 55 | 58 | 60 |
人數 | 2 | 5 | 6 | 6 | 8 | 7 | 6 |
根據上表中信息判斷,下列結論中錯誤的是( )
A.該班一共有40名同學
B.該班學生這次考試成績的眾數是55分
C.該班學生這次考試成績的中位數是55分
D.該班學生這次考試成績的平均數是55分
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com