
【題目】[知識回顧]
七年級學習代數(shù)式求值時,遇到這樣一類題 “代數(shù)式![]() 的值與
的值與![]() 的取值無關,求
的取值無關,求![]() 的值”,通常的解題方法是:把
的值”,通常的解題方法是:把![]() 看作字母,
看作字母,![]() 看作系數(shù)合并同類項,因為代數(shù)式的值與
看作系數(shù)合并同類項,因為代數(shù)式的值與![]() 的取值無關,所以含
的取值無關,所以含![]() 項的系數(shù)為
項的系數(shù)為![]() ,即原式
,即原式![]() ,所以
,所以![]() ,則
,則![]() .
.
[理解應用]
![]() 若關于
若關于![]() 的多項式
的多項式![]() 的值與
的值與![]() 的取值無關,試求
的取值無關,試求![]() 的值:
的值:
![]() 若一次函數(shù)
若一次函數(shù)![]() 的圖像經(jīng)過某個定點,則該定點坐標為 ;
的圖像經(jīng)過某個定點,則該定點坐標為 ;
[能力提升]
![]() 張如圖1的小長方形,長為
張如圖1的小長方形,長為![]() ,寬為
,寬為![]() ,按照圖2方式不重疊地放在大矩形
,按照圖2方式不重疊地放在大矩形![]() 內,大矩形中未被覆蓋的兩個部分(圖中陰影部分) ,設右上角的面積為
內,大矩形中未被覆蓋的兩個部分(圖中陰影部分) ,設右上角的面積為![]() ,左下角的面積為
,左下角的面積為![]() ,當
,當![]() 的長變化時,
的長變化時,![]() 的值始終保持不變,求
的值始終保持不變,求![]() 與
與![]() 的等量關系.
的等量關系.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數(shù)學 來源: 題型:
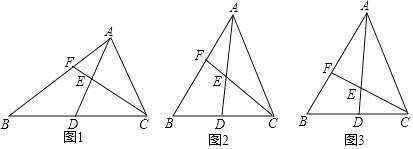
【題目】在△ABC中,AD為BC邊上的中線,E為AD上一動點,設DE=nEA,連接CE并延長,交AB于點F.
(1)嘗試探究:如圖1,當∠BAC=90°,∠B=30°,DE=EA時,BF,BA之間的數(shù)量關系是 ;
(2)類比延伸:如圖2,當△ABC為銳角三角形,DE=EA時,(1)中的結論是否仍然成立?若成立,請給予證明;若不成立,請說明理由;
(3)拓展遷移:如圖3,當△ABC為銳角三角形,DE=nEA時,請直接寫出BF,BA之間的數(shù)量關系.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】△ABC和△CDE都是等腰三角形,∠BAC=∠EDC=120°.
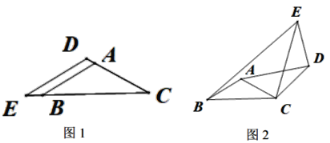
(1)如圖1,A、D、C在同一直線上時,![]() =_______,
=_______,![]() =_______;
=_______;
(2)在圖1的基礎上,固定△ABC,將△CDE繞C旋轉一定的角度α(0°<α<360°),如圖2,連接AD、BE.
① ![]() 的值有沒有改變?請說明理由.
的值有沒有改變?請說明理由.
②拓展研究:若AB=1,DE=![]() ,當 B、D、E在同一直線上時,請計算線段AD的長;
,當 B、D、E在同一直線上時,請計算線段AD的長;
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
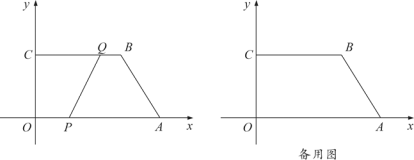
【題目】如圖,在平面直角坐標系中,四邊形OABC的頂點坐標分別為O(0,0),A(6,0),B(4,3),C(0,3).動點P從點O出發(fā),以每秒![]() 個單位長度的速度沿邊OA向終點A運動;動點Q從點B同時出發(fā),以每秒1個單位長度的速度沿邊BC向終點C運動.設運動的時間為t秒,PQ2=y.
個單位長度的速度沿邊OA向終點A運動;動點Q從點B同時出發(fā),以每秒1個單位長度的速度沿邊BC向終點C運動.設運動的時間為t秒,PQ2=y.
(1)直接寫出y關于t的函數(shù)解析式及t的取值范圍: ;
(2)當PQ=![]() 時,求t的值;
時,求t的值;
(3)連接OB交PQ于點D,若雙曲線![]() (k≠0)經(jīng)過點D,問k的值是否變化?若不變化,請求出k的值;若變化,請說明理由.
(k≠0)經(jīng)過點D,問k的值是否變化?若不變化,請求出k的值;若變化,請說明理由.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】已知:在△ABC中,AB=AC,點D是AB上一點,以BD為直徑的⊙0與AC邊相切于點E,交BC于點F,FG⊥AC于點G.
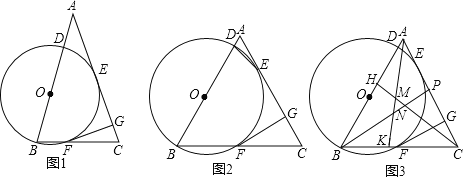
(1)如圖l,求證:GE=GF;
(2)如圖2,連接DE,∠GFC=2∠AED,求證:△ABC為等邊三角形;
(3)如圖3,在(2)的條件下,點H、K、P分別在AB、BC、AC上,AK、BP分別交CH于點M、N,AH=BK,∠PNC﹣![]() ∠BAK=60°,CN=6,CM=4
∠BAK=60°,CN=6,CM=4![]() ,求BC的長.
,求BC的長.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
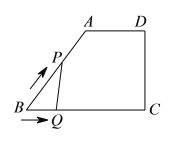
【題目】如圖,在四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,動點
,動點![]() ,
,![]() 同時從點
同時從點![]() 出發(fā),點
出發(fā),點![]() 以
以![]() 的速度沿折線
的速度沿折線![]() 運動到點
運動到點![]() ,點
,點![]() 以
以![]() 的速度沿
的速度沿![]() 運動到點
運動到點![]() ,設
,設![]() ,
,![]() 同時出發(fā)
同時出發(fā)![]() 時,
時,![]() 的面積為
的面積為![]() ,則
,則![]() 與
與![]() 的函數(shù)圖象大致是( )
的函數(shù)圖象大致是( )
A. 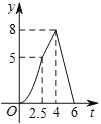 B.
B. 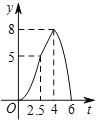
C. 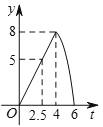 D.
D. 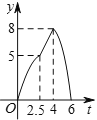
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】已知函數(shù)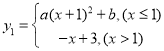 (
(![]() 為常數(shù)且
為常數(shù)且![]() ),已知當
),已知當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ,請對該函數(shù)及其圖像進行如下探究:
,請對該函數(shù)及其圖像進行如下探究:

(1)求函數(shù)![]() 的解析式;
的解析式;
(2)如圖,請在平面直角坐標系中,畫出該函數(shù)的圖像;
(3)結合所畫函數(shù)圖像,請寫出該函數(shù)的一條性質;
(4)解決問題:若函數(shù)![]() 與
與![]() 至少有兩個公共點,請直接寫出
至少有兩個公共點,請直接寫出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com