
【題目】綜合題。
(1)問題發現:如圖1,△ACB和△DCE均為等邊三角形,點A,D,E在同一直線上,連接BE.
①∠AEB的度數為
②猜想線段AD,BE之間的數量關系為: , 并證明你的猜想.
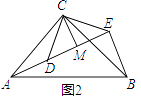
(2)拓展探究:如圖2,△ACB和△DCE均為等腰直角三角形,∠ACB=∠DCE=90°,點A,D,E在同一直線上,CM 為△DCE中DE邊上的高,連接BE,請求出∠AEB的度數及線段CM,AE,BE 之間的數量關系.
【答案】
(1)60°;AD=BE
(2)
解:∠AEB=90°,AE﹣BE=2CM,
證明:∵△DCE是等腰直角三角形,CM是中線,
∴CM=DM=EM= ![]() DE,
DE,
在△ACD和△BCE中,
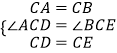 ,
,
∴△ACD≌△BCE,
∴∠CDA=∠CEB,
∵∠CDA=135°,
∴∠AEB=135°﹣45°=90°,
∴BE=AD,
∴AE﹣AD=DE=2CM,
∴AE﹣BE=2CM.
【解析】解:(1)①∵△ACB和△DCE均為等邊三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB﹣∠DCB=∠DCE﹣∠DCB,即∠ACD=∠BCE,
在△ACD和△BCE中,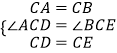 ,
,
∴△ACD≌△BCE,
∴∠CEB=∠CDA=120°,
∴∠AEB=60°,
所以答案是:60°;②AD=BE,
證明:∵△ACD≌△BCE,
∴AD=BE,
所以答案是:AD=BE;


科目:初中數學 來源: 題型:
【題目】計算:
(1)2a(b2c3)2·(-2a2b)3;
(2)(2x-1)2-x(4x-1);
(3)632+2×63×37+372.(用簡便方法)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一個不透明的布袋中,有紅球、白球共30個,除顏色外其它完全相同,小明通過多次摸球試驗后發現,其中摸到紅球的頻率穩定在40%,則隨機從口袋中摸出一個是紅球的概率是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小紅在數學課上學習了角的相關知識后,立即對角產生了濃厚的興趣.她查閱書籍發現兩個有趣的概念,三角形中相鄰兩條邊的夾角叫做三角形的內角;三角形一條邊的延長線與其鄰邊的夾角,叫做三角形的外角.小紅還了解到三角形的內角和是180°,同時她很容易地證明了三角形外角的性質,即三角形的一個外角等于與它不相鄰的兩個內角的和.于是,愛思考的小紅在想,三角形的內角是否也具有類似的性質呢?三角形的一個內角與它不相鄰的兩個外角的和之間存在怎樣的數量關系呢?

①嘗試探究:
(1)如圖1,∠1與∠2分別為△ABC的兩個外角,試探究∠A與∠1+∠2之間存在怎樣的數量關系?為什么?
解:數量關系:∠l+∠2=180°+∠A
理由:∵∠1與∠2分別為△ABC的兩個外角
∴∠1=180°-∠3,∠2=180°-∠4
∴∠1+∠2=360°-(∠3+∠4)
∵三角形的內角和為180°
∴∠3+∠4=180°-∠A
∴∠l+∠2=360°-(180°-∠A)=180°+∠A
小紅順利地完成了探究過程,并想考一考同學們,請同學們利用上述結論完成下面的問題.
②初步應用:
(2)如圖2,在△ABC紙片中剪去△CED,得到四邊形ABDE,∠1=130°,則∠2-∠C=________;
(3)如圖3,在△ABC中,BP、CP分別平分外角∠DBC、∠ECB,則∠P與∠A有何數量關系?________________.(直接填答案)
③拓展提升:
(4)如圖4,在四邊形ABCD中,BP、CP分別平分外角∠EBC、∠FCB,則∠P與∠1、∠2有何數量關系?為什么?(若需要利用上面的結論說明,可直接使用,不需說明理由.)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,AC=BC=1,將Rt△ABC繞點A逆時針旋轉30°后得到Rt△ADE,點B經過的路徑為弧BD,則圖中陰影部分的面積是________.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com