
【題目】在△ABC中,AB=AC,∠A=60°,點D是BC邊的中點,作射線DE,與邊AB交于點E,射線DE繞點D順時針旋轉120°,與直線AC交于點F.
(1)依題意將圖1補全;
(2)小華通過觀察、實驗提出猜想:在點E運動的過程中,始終有DE=DF.小華把這個猜想與同學們進行交流,通過討論,形成了證明該猜想的幾種想法:
想法1:由點D是BC邊的中點,通過構造一邊的平行線,利用全等三角形,可證DE=DF;
想法2:利用等邊三角形的對稱性,作點E關于線段AD的對稱點P,由∠BAC與∠EDF互補,可得∠AED與∠AFD互補,由等角對等邊,可證DE=DF;
想法3:由等腰三角形三線合一,可得AD是∠BAC的角平分線,由角平分線定理,構造點D到AB,AC的高,利用全等三角形,可證DE=DF….
請你參考上面的想法,幫助小華證明DE=DF(選一種方法即可);
(3)在點E運動的過程中,直接寫出BE,CF,AB之間的數量關系.
【答案】
(1)
解:如圖1所示:
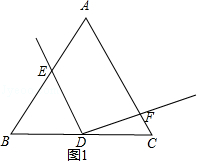
(2)
解:想法1證明:如圖2,過D作DG∥AB,交AC于G,
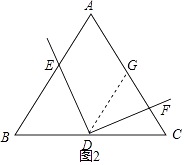
∵點D是BC邊的中點,
∴DG= ![]() AB,
AB,
∴△CDG是等邊三角形,
∴∠EDB+∠EDG=120°,
∵∠FDG+∠EDG=120°,
∴∠EDB=∠FDG,
∵BD=DG,∠B=∠FGD=60°,
∴△BDE≌△GDF,
∴DE=DF;
想法2證明:如圖3,連接AD,
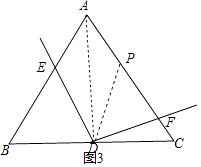
∵點D是BC邊的中點,
∴AD是△ABC的對稱軸,
作點E關于線段AD的對稱點P,點P在邊AC上,
∴△ADE≌△ADP,
∴DE=DP,∠AED=∠APD,
∵∠BAC+∠EDF=180°,
∴∠AED+∠AFD=180°,
∵∠APD+∠DPF=180°,
∴∠AFD=∠DPF,
∴DP=DF,
∴DE=DF;
想法3證明:如圖4,連接AD,過D作DM⊥AB于M,DN⊥AC于N,

∵點D是BC邊的中點,
∴AD平分∠BAC,
∵DM⊥AB于M,DN⊥AC于N,
∴DM=DN,
∵∠A=60°,
∴∠MDE+∠EDN=120°,
∵∠FDN+∠EDN=120°,
∴∠MDE=∠FDN,
∴Rt△MDE≌Rt△NDF,
∴DE=DF
(3)
解:當點F在AC邊上時,BE+CF= ![]() AB,
AB,
當點F在AC延長線上時,BE﹣CF= ![]() AB,
AB,
證明:①當點F在AC邊上時,如圖5中,過點D作DM⊥AB于M,作DN⊥AC于N.

∵∠B=∠C=60°,BD=DC,∠BDM=∠CDN=30°,
在△BDM與△CDN中, 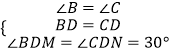 ,
,
∴△BDM≌△CDN,
∴BM=CN,DM=DN,
又∵∠EDF=120°=∠MDN,
∴∠EDM=∠NDF,
又∵∠EMD=∠FND=90°,
∴△EDM≌△FDN,
∴ME=NF,
∴BE+CF=BM+EM+NC﹣FN=2BM=BD= ![]() AB;
AB;
②當點F在AC延長線上時,如圖6,
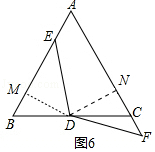
∵∠B=∠C=60°,BD=DC,∠BDM=∠CDN=30°,
∴△BDM≌△CDN,
∴BM=CN,DM=DN,
又∵∠EDF=120°=∠MDN,
∴∠EDM=∠NDF,
又∵∠EMD=∠FND=90°,
∴△EDM≌△FDN,
∴ME=NF,
∴BE﹣CF=BM+EM﹣(FN﹣CN)=2BM=BD= ![]() AB,
AB,
綜上所述:當點F在AC邊上時,BE+CF= ![]() AB;
AB;
當點F在AC延長線上時,BE﹣CF= ![]() AB.
AB.
【解析】(1)根據題目中的要求作圖即可;(2)想法1,由已知得到△CDG是等邊三角形,證得∠EDB=∠FDG,根據全等三角形的性質即可得到結論;想法2,如圖3,連接AD,作點E關于線段AD的對稱點P,點P在邊AC上,根據全等三角形的性質得到DE=DP,∠AED=∠APD,等量代換得到∠AFD=∠DPF,于是得到結論;想法3,如圖4,連接AD,過D作DM⊥AB于M,DN⊥AC于N,根據角平分線的性質得到DM=DN,根據全等三角形的性質即可得到結論;(3)當點F在AC邊上時,過點D作DM⊥AB于M,作DN⊥AC于N.只要證明△BDM≌△CDN,△EDM≌△FDN即可解決問題,當點F在AC延長線上時,證明方法類似.


科目:初中數學 來源: 題型:
【題目】有一種公益叫“光盤”.所謂“光盤”,就是吃光你盤子中的食物,杜絕“舌尖上的浪費”.某校九年級開展“光盤行動”宣傳活動,根據各班級參加該活動的總人次折線統計圖,下列說法正確的是( )

A. 極差是40 B. 中位數是58 C. 平均數大于58 D. 眾數是5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,AB=4,AD=6.M、N分別是AB、CD邊的中點,P是AD上的點,且∠PNB=3∠CBN.
(1)求證:∠PNM=2∠CBN;
(2)求線段AP的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將矩形ABCD繞點A按逆時針方向旋轉,得到矩形AEFG,E點正好落在邊CD上,連接BE,BG,且BG交AE于P.
(1)求證:∠CBE=![]() ∠BAE;
∠BAE;
(2)求證:PG=PB;
(3)若AB=![]() ,BC=3,求出BG的長.
,BC=3,求出BG的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】填空或填寫理由.
(1)如圖甲,∵∠ =∠ (已知);
∴AB∥CD( )
(2)如圖乙,已知直線a∥b,∠3=80°,求∠1,∠2的度數.
解:∵a∥b,( )
∴∠1=∠4( )
又∵∠3=∠4( )
∠3=80°(已知)
∴∠1=( )(等量代換)
又∵∠2+∠3=180°
∴∠2=( )(等式的性質)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知平行四邊形ABCD中,CE平分∠BCD且交AD于點E,A F∥CE,且交BC于點F.
(1)求證:△ABF≌△CDE;
(2)如圖,若∠1=65°,求∠B的大小.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知點A從點(1,0)出發,以1個單位長度/秒的速度沿x軸向正方向運動,以O、A為頂點作菱形OABC,使點B、C在第一象限內,且∠AOC=60°,點P的坐標為(0,3),設點A運動了t秒,求:
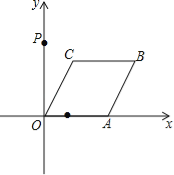
(1)點C的坐標(用含t的代數式表示);
(2)點A在運動過程中,當t為何值時,使得△OCP為等腰三角形?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下面材料:
在數學課上,老師提出如下問題:
作圖:過直線外一點作已知直線的平行線.
已知:直線l及其外一點A.
求作:l的平行線,使它經過點A.

小天利用直尺和三角板進行如下操作:如圖所示:
①用三角板的斜邊與已知直線l重合;
②用直尺緊靠三角板一條直角邊;
③沿著直尺平移三角板,使三角板的斜邊通過已知點A;
④沿著這條斜邊畫一條直線,所畫直線與已知直線平行.
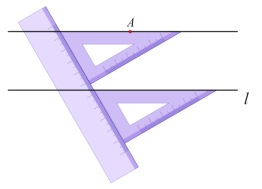
老師說:“小天的作法正確.”
請回答:小天的作圖依據是___________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩名隊員參加射擊訓練,成績分別被制成下列兩個統計圖:
根據以上信息,整理分析數據如下:
平均成績/環 | 中位數/環 | 眾數/環 | 方差 | |
甲 | a | 7 | 7 | 1.2 |
乙 | 7 | b | 8 | c |
(1)寫出表格中a,b,c的值;
(2)分別運用表中的四個統計量,簡要分析這兩名隊員的射擊訓練成績.若選派其中一名參賽,你認為應選哪名隊員?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com