
【題目】如圖,已知△ABC中AB=AC.
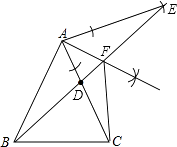
(1)作圖:在AC上有一點D,延長BD,并在BD的延長線上取點E,使AE=AB,連AE,作∠EAC的平分線AF,AF交DE于點F(用尺規作圖,保留作圖痕跡,不寫作法);
(2)在(1)的條件下,連接CF,求證:∠E=∠ACF.
【答案】
(1)解:如圖所示;
(2)證明:∵AB=AC,AE=AB,
∴AE=AC,
∵AF是∠EAC的平分線,
∴∠EAF=∠CAF,
在△AEF和△ACF中,
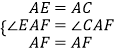 ,
,
∴△AEF≌△ACF(SAS),
∴∠E=∠ACF.
【解析】(1)以點A為圓心,以AB長為半徑畫弧,與BD的延長線的交點即為點E,再以A點為圓心,以任意長為半徑畫弧,分別與AC,AE相交,然后以這兩點為圓心,以大于它們![]() 長度為半徑畫弧,兩弧相交于一點,過點A與這一點作出射線與BE的交點即為所求的點F;
長度為半徑畫弧,兩弧相交于一點,過點A與這一點作出射線與BE的交點即為所求的點F;
(2)根據等量代換得出AE=AC,根據角平分線的定義得出∠EAF=∠CAF,然后利用SAS判斷出△AEF≌△ACF,根據全等三角形對應角相等得出答案。


科目:初中數學 來源: 題型:
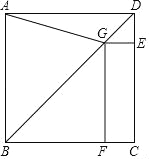
【題目】如圖,在正方形ABCD中,點G在對角線BD上(不與點B,D重合),GE⊥DC于點E,GF⊥BC于點F,連結AG.
(1)寫出線段AG,GE,GF長度之間的數量關系,并說明理由;
(2)若正方形ABCD的邊長為1,∠AGF=105°,求線段BG的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】 在平面直角坐標系中,借助直角三角板可以找到一元二次方程的實數根.比如對于方程![]() ,操作步驟是:
,操作步驟是:
第一步:根據方程的系數特征,確定一對固定點![]() ;
;
第二步:在坐標平面中移動一個直角三角板,使一條直角邊恒過點![]() ,另一條直角邊恒過點
,另一條直角邊恒過點![]() ;
;
第三步:在移動過程中,當三角板的直角頂點落在![]() 軸上點
軸上點![]() 處時,點
處時,點![]() 的橫坐標
的橫坐標![]() 即為該方程的一個實數根(如圖1);
即為該方程的一個實數根(如圖1);
第四步:調整三角板直角頂點的位置,當它落在![]() 軸上另—點
軸上另—點![]() 處時,點
處時,點![]() 的橫坐標
的橫坐標![]() 即為該方程的另一個實數根.
即為該方程的另一個實數根.

(1)在圖2中,按照“第四步”的操作方法作出點![]() (請保留作出點
(請保留作出點![]() 時直角三角板兩條直角邊的痕跡);
時直角三角板兩條直角邊的痕跡);
(2)結合圖1,請證明“第三步”操作得到的![]() 就是方程
就是方程![]() 的一個實數根;
的一個實數根;
(3)上述操作的關鍵是確定兩個固定點的位置,若要以此方法找到一元二次方程![]()
![]() 的實數根,請你直接寫出一對固定點的坐標;
的實數根,請你直接寫出一對固定點的坐標;
(4)實際上,(3)中的固定點有無數對,一般地,當![]() 與
與![]() 之間滿足怎樣的關系時,點
之間滿足怎樣的關系時,點![]() 就是符合要求的—對固定點?
就是符合要求的—對固定點?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com