
如圖,若銳角△ABC內接于⊙O,點D在⊙O外(與點C在AB同側),則下列三個結論:①sin∠C>sin∠D;②cos∠C>cos∠D;③tan∠C>tan∠D中,正確的結論為( )
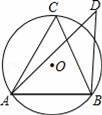

A.①② B.②③ C.①②③ D.①③
科目:初中數學 來源: 題型:
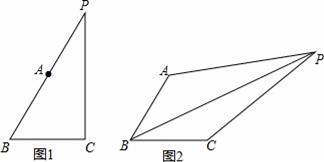
.數學活動課上,老師提出這樣一個問題:如果AB=BC,∠ABC=60°,∠APC=30°,連接PB,那么PA、PB、PC之間會有怎樣的等量關系呢?經過思考后,部分同學進行了如下的交流:
小蕾:我將圖形進行了特殊化,讓點P在BA延長線上(如圖1),得到了一個猜想:PA2+PC2=PB2.
小東:我假設點P在∠ABC的內部,根據題目條件,這個圖形具有“共端點等線段”的特點,可以利用旋轉解決問題,旋轉△PAB后得到△P′CB,并且可推出△PBP′,△PCP′分別是等邊三角形、直角三角形,就能得到猜想和證明方法.
這時老師對同學們說,請大家完成以下問題:
(1)如圖2,點P在∠ABC的內部,
①PA=4,PC=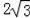
 ,PB= .
,PB= .
②用等式表示PA、PB、PC之間的數量關系,并證明.
(2)對于點P的其他位置,是否始終具有②中的結論?若是,請證明;若不是,請舉例說明.

查看答案和解析>>
科目:初中數學 來源: 題型:
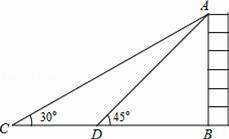
如圖,某校數學興趣小組為測得大廈AB的高度,在大廈前的平地上選擇一點C,測得大廈頂端A的仰角為30°,再向大廈方向前進80米,到達點D處(C、D、B三點在同一直線上),又測得大廈頂端A的仰角為45°,請你計算該大廈的高度.(精確到0.1米,參考數據: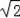
 ≈1.414,
≈1.414,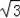
 ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中數學 來源: 題型:
如圖,在平面直角坐標系中,已知△ABC的三個頂點的坐標分別為A(﹣5,1),B(﹣2,2),C(﹣1,4),請按下列要求畫圖:
(1)將△ABC先向右平移4個單位長度、再向下平移1個單位長度,得到△A1B1C1,畫出△A1B1C1;
(2)△A2B2C2與△ABC關于原點O成中心對稱,畫出△A2B2C2.


查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com