
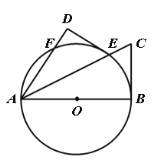
【題目】如圖,已知AB是⊙O的直徑,F是⊙O上一點,∠BAF的平分線交⊙O于點E,交⊙O的切線BC于點C,過點E作ED⊥AF,交AF的延長線于點D.
(1)求證:DE是⊙O的切線;
(2)若DE=3,CE=2,
①求![]() 值;
值;
②若點G 為AE上一點,求OG+![]() EG最小值.
EG最小值.
【答案】(1)證明見解析(2)①![]() ②3
②3
【解析】
(1)作輔助線,連接OE.根據切線的判定定理,只需證DE⊥OE即可;
(2)①連接BE.根據BC、DE兩切線的性質證明△ADE∽△BEC;又由角平分線的性質、等腰三角形的兩個底角相等求得△ABE∽△AFD,所以![]() ;
;
②連接OF,交AD于H,由①得∠FOE=∠FOA=60°,連接EF,則△AOF、△EOF都是等邊三角形,故四邊形AOEF是菱形,由對稱性可知GO=GF,過點G作GM⊥OE于M,則GM=![]() EG,OG+
EG,OG+![]() EG=GF+GM,根據兩點之間線段最短,當F、G、M三點共線,OG+
EG=GF+GM,根據兩點之間線段最短,當F、G、M三點共線,OG+![]() EG=GF+GM=FM最小,此時FM =3.故OG+
EG=GF+GM=FM最小,此時FM =3.故OG+![]() EG最小值是3.
EG最小值是3.
(1)連接OE
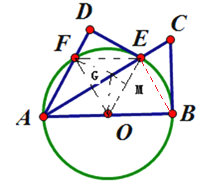
∵OA=OE,∴∠AEO=∠EAO
∵∠FAE=∠EAO,∴∠FAE=∠AEO
∴OE∥AF
∵DE⊥AF,∴OE⊥DE
∴DE是⊙O的切線
(2)①解:連接BE
∵直徑AB ∴∠AEB=90°
∵圓O與BC相切
∴∠ABC=90°
∵∠EAB+∠EBA=∠EBA+∠CBE=90°
∴∠EAB=∠CBE
∴∠DAE=∠CBE
∵∠ADE=∠BEC=90°
∴△ADE∽△BEC
∴![]()
②連接OF,交AD于H,
由①,設BC=2x,則AE=3x
∵△BEC∽△ABC ∴![]()
∴![]()
解得:x1=2,![]() (不合題意,舍去)
(不合題意,舍去)
∴AE=3x=6,BC=2x=4,AC=AE+CE=8
∴AB=![]() ,∠BAC=30°
,∠BAC=30°
∴∠AEO=∠EAO=∠EAF=30°,∴∠FOE=2∠FAE=60°
∴∠FOE=∠FOA=60°,連接EF,則△AOF、△EOF都是等邊三角形,∴四邊形AOEF是菱形
由對稱性可知GO=GF,過點G作GM⊥OE于M,則GM=![]() EG,OG+
EG,OG+![]() EG=GF+GM,根據兩點之間線段最短,當F、G、M三點共線,OG+
EG=GF+GM,根據兩點之間線段最短,當F、G、M三點共線,OG+![]() EG=GF+GM=FM最小,此時FM=FOsin60o=3.
EG=GF+GM=FM最小,此時FM=FOsin60o=3.
故OG+![]() EG最小值是3.
EG最小值是3.


科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=﹣x2+bx+c與一直線相交于A(1,0)、C(﹣2,3)兩點,與y軸交于點N,其頂點為D.
(1)求拋物線及直線AC的函數關系式;
(2)若P是拋物線上位于直線AC上方的一個動點,求△APC的面積的最大值及此時點P的坐標;
(3)在對稱軸上是否存在一點M,使△ANM的周長最小.若存在,請求出M點的坐標和△ANM周長的最小值;若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,AB為半圓O的直徑,D為BA的延長線上一點,DC為半圓O的切線,切點為C.
(1)求證:∠ACD=∠B;
(2)如圖2,∠BDC的平分線分別交AC,BC于點E,F;
①求tan∠CFE的值;
②若AC=3,BC=4,求CE的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
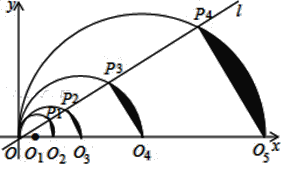
【題目】如圖,在平面直角坐標系中,直線l的函數表達式為y=![]() x,點O1的坐標為(1,0),以O1為圓心,O1O為半徑畫半圓,交直線l于點P1,交x軸正半軸于點O2,由弦P1O2和
x,點O1的坐標為(1,0),以O1為圓心,O1O為半徑畫半圓,交直線l于點P1,交x軸正半軸于點O2,由弦P1O2和![]() 圍成的弓形面積記為S1,以O2為圓心,O2O為半徑畫圓,交直線l于點P2,交x軸正半軸于點O3,由弦P2O3和圍
圍成的弓形面積記為S1,以O2為圓心,O2O為半徑畫圓,交直線l于點P2,交x軸正半軸于點O3,由弦P2O3和圍![]() 成的弓形面積記為S2,以O3為圓心,O3O為半徑畫圓,交直線l于點P3,交x軸正半軸于點O4,由弦P3O4和
成的弓形面積記為S2,以O3為圓心,O3O為半徑畫圓,交直線l于點P3,交x軸正半軸于點O4,由弦P3O4和![]() 圍成的弓形面積記為S3;…按此做法進行下去,其中S2018的面積為__________.
圍成的弓形面積記為S3;…按此做法進行下去,其中S2018的面積為__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
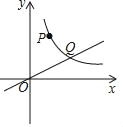
【題目】如圖所示,直線y=![]() x與反比例函數y=
x與反比例函數y=![]() (k≠0,x>0)的圖象交于點Q(4,a),點P(m,n)是反比例函數圖象上一點,且n=2m.
(k≠0,x>0)的圖象交于點Q(4,a),點P(m,n)是反比例函數圖象上一點,且n=2m.
(1)求點 P坐標;
(2)若點M在x軸上,使得△PMQ的面積為3,求M坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(問題解決)
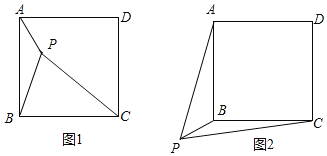
一節數學課上,老師提出了這樣一個問題:如圖1,點P是正方形ABCD內一點,PA=1,PB=2,PC=3.你能求出∠APB的度數嗎?
小明通過觀察、分析、思考,形成了如下思路:
思路一:將△BPC繞點B逆時針旋轉90°,得到△BP′A,連接PP′,求出∠APB的度數;
思路二:將△APB繞點B順時針旋轉90°,得到△CP'B,連接PP′,求出∠APB的度數.
請參考小明的思路,任選一種寫出完整的解答過程.
(類比探究)
如圖2,若點P是正方形ABCD外一點,PA=3,PB=1,PC=![]() ,求∠APB的度數.
,求∠APB的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,我們定義直線![]() 為拋物線
為拋物線![]() 、b、c為常數,
、b、c為常數,![]() 的“夢想直線”;有一個頂點在拋物線上,另有一個頂點在y軸上的三角形為其“夢想三角形”.
的“夢想直線”;有一個頂點在拋物線上,另有一個頂點在y軸上的三角形為其“夢想三角形”.

已知拋物線![]() 與其“夢想直線”交于A、B兩點
與其“夢想直線”交于A、B兩點![]() 點A在點B的左側
點A在點B的左側![]() ,與x軸負半軸交于點C.
,與x軸負半軸交于點C.
![]() 填空:該拋物線的“夢想直線”的解析式為______,點A的坐標為______,點B的坐標為______;
填空:該拋物線的“夢想直線”的解析式為______,點A的坐標為______,點B的坐標為______;
![]() 如圖,點M為線段CB上一動點,將
如圖,點M為線段CB上一動點,將![]() 以AM所在直線為對稱軸翻折,點C的對稱點為N,若
以AM所在直線為對稱軸翻折,點C的對稱點為N,若![]() 為該拋物線的“夢想三角形”,求點N的坐標;
為該拋物線的“夢想三角形”,求點N的坐標;
![]() 當點E在拋物線的對稱軸上運動時,在該拋物線的“夢想直線”上,是否存在點F,使得以點A、C、E、F為頂點的四邊形為平行四邊形?若存在,請直接寫出點E、F的坐標;若不存在,請說明理由.
當點E在拋物線的對稱軸上運動時,在該拋物線的“夢想直線”上,是否存在點F,使得以點A、C、E、F為頂點的四邊形為平行四邊形?若存在,請直接寫出點E、F的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
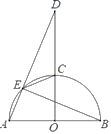
【題目】如圖,已知AB是半圓O的直徑,OC⊥AB交半圓于點C,D是射線OC上一點,連結AD交半圓O于點E,連結BE,CE.
(1)求證:EC平分∠BED.
(2)當EB=ED時,求證:AE=CE.
查看答案和解析>>
科目:初中數學 來源: 題型:
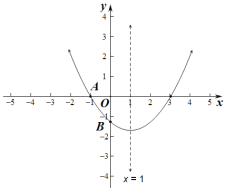
【題目】如圖,已知二次函數![]() 的圖象與
的圖象與![]() 軸交于點
軸交于點![]() (-1,0),與
(-1,0),與![]() 軸的交點在
軸的交點在![]() (0,-2)和(0,-1)之間(不包括這兩點),對稱軸為直線
(0,-2)和(0,-1)之間(不包括這兩點),對稱軸為直線![]() ,下列結論不正確的是( )
,下列結論不正確的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com