
分析 (1)根據方程的系數結合根的判別式即可得出△=(m-1)2≥0,由此即可證出無論m取什么數,方程總有兩個實數根;
(2)將x=2代入原方程可得出關于m的一元一次方程,解之即可得出m的值,設方程的另一根為x0,根據根與系數的關系即可得出關于x0的一元一次方程,解之即可得出方程的另一個實數根.
解答 (1)證明:∵在方程x2-mx+$\frac{m}{2}$-$\frac{1}{4}$=0中,△=(-m)2-4×1×($\frac{m}{2}-\frac{1}{4}$)=m2-2m+1=(m-1)2≥0,
∴無論m取什么數,方程總有兩個實數根;
(2)解:將x=2代入原方程得:4-2m+$\frac{m}{2}$-$\frac{1}{4}$=0,
解得:m=$\frac{5}{2}$.
設方程的另一根為x0,
則有:2+x0=m=$\frac{5}{2}$,
∴x0=$\frac{1}{2}$.
∴若已知方程有一個實數根是2,則另一個實數根為$\frac{1}{2}$.
點評 本題考查了根與系數的關系以及根的判別式,解題的關鍵是:(1)根據根的判別式找出△=(m-1)2≥0;(2)將x=2代入原方程求出m的值.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:填空題
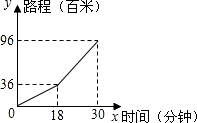 小明早晨從進學校騎車到學校,先上坡后下坡,行程情況如圖所示,若返回時上坡、下坡的速度和原來相同,那么小亮從學校騎車回家用的時間是37.2分鐘.
小明早晨從進學校騎車到學校,先上坡后下坡,行程情況如圖所示,若返回時上坡、下坡的速度和原來相同,那么小亮從學校騎車回家用的時間是37.2分鐘.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖一架云梯AB斜靠在一面墻上,梯子的底端B離墻根O的距離OB長為7米,梯子的頂端A到地面的距離OA為24米.
如圖一架云梯AB斜靠在一面墻上,梯子的底端B離墻根O的距離OB長為7米,梯子的頂端A到地面的距離OA為24米.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
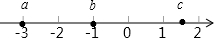 已知有理數a,b,c在數軸上的位置如圖所示,則下列說法中不正確的是( )
已知有理數a,b,c在數軸上的位置如圖所示,則下列說法中不正確的是( )| A. | a=-3 | B. | b=-1 | C. | a的相反數為正數 | D. | c可能等于2.5 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com