D
分析:分別根據全等三角形的判定方法由兩個等腰直角三角形的性質,分別假設已知條件證明即可.
解答:
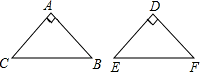
解:∵△ACB和△DEF是兩個等腰直角三角形,
∴∠A=∠D=90°,AC=AB,DE=DF,
當AC=DE,AB=DF,BC=EF,
∴

,
∴△ACB≌△DEF(SSS);故選項①正確;
∵△ACB和△DEF是兩個等腰直角三角形,
∴當∠C=∠B=45°,∠E=∠F=45°,
∵AC=DE,AB=DF,
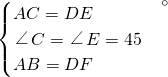
,
∴△ACB≌△DEF(SAS),故選項②正確;
∵△ACB和△DEF是兩個等腰直角三角形,
∴當∠C=∠B=45°,∠E=∠F=45°,
∵AC=DE,
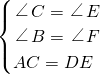
,
∴△ACB≌△DEF(AAS),故選項③正確;
∵△ACB和△DEF是兩個等腰直角三角形,
∴當∠C=∠E=45°,AC=DE,AB=DF,

,
∴△ACB≌△DEF(SSA),故選項④正確;
∵△ACB和△DEF是兩個等腰直角三角形,
∴當∠C=∠E=45°,∠A=∠D=90°,AC=DE,

,
∴△ACB≌△DEF(ASA),故選項⑤正確;
∵△ACB和△DEF是兩個等腰直角三角形,
∴當∠A=∠D=90°,AC=DE,BC=EF,
在Rt△ACB和Rt△DEF中,

,
∴Rt△ACB≌Rt△DEF(HL),故選項⑥正確;
故①②③④⑤⑥都正確一共6個.
故選:D.
點評:此題主要考查了全等三角形的判定方法的應用,由兩個等腰直角三角形得出已知條件進而判定得出是解題關鍵.

 解:∵△ACB和△DEF是兩個等腰直角三角形,
解:∵△ACB和△DEF是兩個等腰直角三角形, ,
,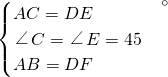 ,
,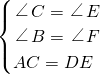 ,
, ,
, ,
, ,
,

 應用題點撥系列答案
應用題點撥系列答案 狀元及第系列答案
狀元及第系列答案 同步奧數系列答案
同步奧數系列答案