Rt△ABC中，∠C=90°，點D、E分別是△ABC邊AC、BC上的點，點P是一動點．令∠PDA=∠1，∠PEB=∠2，∠DPE=∠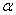
．
（1）若點P在線段AB上，如圖（1）所示，且∠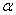=50°，則∠1+∠2= °；（2分）
（2）若點P在邊AB上運動，如圖（2）所示，則∠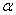、∠1、∠2之間的關系為： ；（2分）
（3）若點P運動到邊AB的延長線上，如圖（3）所示，則∠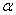、∠1、∠2之間有何關系？猜想并說明理由．（6分）
（4）若點P運動到△ABC形外，如圖（4）所示，則∠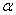、∠1、∠2之間的關系為： ．（2分）
科目：初中數學 來源： 題型：
如圖，以△ABC的三邊為邊，在BC的同側分別作3個等邊三角形，即△ABD、△BCE、△ACF。
（1）求證：四邊形ADEF是平行四邊形？
（2）當△ABC滿足什么條件時，四邊形ADEF是矩形，并說明理由。
（3）當△ABC滿足什么條件時，四
邊形ADEF是菱形，并說明理由。
（4）當△ABC滿足什么條件時，四邊形ADEF是正方形，不要說明理由。
查看答案和解析>>
科目：初中數學 來源： 題型：
如圖，已知點A、B、C、D在一條直線上，EC∥FD，∠F＝∠E，
求證：AE∥BF．
請在下列空格內填寫結論和理由，完成證明過程：
∵EC∥FD( )，
∴∠F＝∠ ( )．
∵∠F＝∠E(已知)，
∴∠ ＝∠E（等量代換
）．
∴ ∥ ( )．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
∠2+α， （4）∠2=90°+∠1-α，
則它的周長是 
。
次，有
次正面向上，當她擲第11次時，正面向上的概率__.
C．
D．
B．
D．
