試題分析:(1)先根據等邊三角形的性質得到AC=BC,DC=EC,∠ACB=∠DCE=60°,即可得到∠ACD=∠BCE,從而可以證得結論;
(2)過點C作CH⊥BQ于H,根據等邊三角形及角平分線的性質可得∠DAC=30°,再根據△ACD≌△BCE可得∠QBC=∠DAC=30°,根據含30°的直角三角形的性質可得CH的長,最后根據勾股定理求解即可.
(1)∵△ABC與△DCE是等邊三角形,
∴AC=BC,DC=EC,∠ACB=∠DCE=60°,
∴∠ACD+∠DCB=∠ECB+∠DCB=60°,
∴∠ACD=∠BCE,
∴△ACD≌△BCE(SAS);
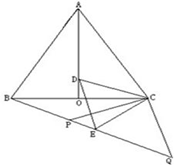
(2)過點C作CH⊥BQ于H,
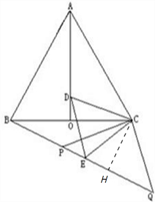
∵△ABC是等邊三角形,AO是角平分線,
∴∠DAC=30°,
∵△ACD≌△BCE,
∴∠QBC=∠DAC=30°,
∴CH=
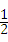
BC=
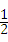
×8=4,
∵PC=CQ=5,CH=4,
∴PH=QH=3,
∴PQ=6.
點評:本題知識點多,綜合性較強,但難度不大,是中考常見題,正確作出輔助線構造直角三角形是解題的關鍵.


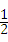 BC=
BC=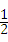 ×8=4,
×8=4,

