
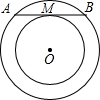
 如圖,已知兩同心圓,大圓的弦AB切小圓于M,若環形的面積為9π,則AB的長是6.
如圖,已知兩同心圓,大圓的弦AB切小圓于M,若環形的面積為9π,則AB的長是6. 分析 環形的面積為9π,就是大圓面積-小圓的面積,根據圓的面積公式,可得π×OA2-π×OM2=9π,解得OA2-OM2=9,再根據勾股定理可知就是AM的平方,所以AM=3,AB=6.
解答 解:連接OA、OM,如圖所示: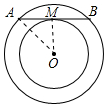
∵大圓的弦AB切小圓于M,
∴AB⊥OM,
∴AM=BM,
∵環形的面積為9π,
根據圓的面積公式可得:π×OA2-π×OM2=9π,
解得:OA2-OM2=9,
根據勾股定理可知:AM2=OA2-OM2,
∴AM=3,
∴AB=2AM=6.
點評 本題考查了切線的性質、垂徑定理、勾股定理;做本題的關鍵是把OA2-OM2=9當成一個整體來計算,并理解9就是AM的平方,從而求出AM,AB的值.


科目:初中數學 來源: 題型:選擇題
套餐類型 | 月費(元/月) | 套餐內包含內容 | 套餐外資費 | ||
| 國內數據流量 | 國內電話(分鐘) | 流量 | 國內 電話 | ||
| 套餐1 | 76 | 400M | 200 | 0M-200M時,0.3元/M 201M-1G時,60元 | 0.15元/分鐘 |
| 套餐2 | 106 | 800M | 300 | ||
| 套餐3 | 136 | 1G | 500 | ||
| 套餐4 | 166 | 2G | 500 | ||
| A. | 套餐1 | B. | 套餐2 | C. | 套餐3 | D. | 套餐4 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
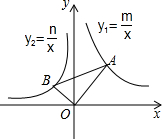 如圖,在平面直角坐標系中,∠AOB=90°,∠OAB=30°,反比例函數y1=$\frac{m}{x}$的圖象經過點A,反比例函數y2=$\frac{n}{x}$的圖象經過點B,則下列關于m,n的關系正確的是( )
如圖,在平面直角坐標系中,∠AOB=90°,∠OAB=30°,反比例函數y1=$\frac{m}{x}$的圖象經過點A,反比例函數y2=$\frac{n}{x}$的圖象經過點B,則下列關于m,n的關系正確的是( )| A. | m=$\frac{\sqrt{3}}{3}$n | B. | m=-$\sqrt{3}$n | C. | m=-$\frac{\sqrt{3}}{3}$n | D. | m=-3n |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
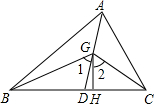 如圖,在△ABC中,AD是它的角平分線,G是AD上的一點,BG,CG分別平分∠ABC,∠ACB,GH⊥BC,垂足為H,求證:
如圖,在△ABC中,AD是它的角平分線,G是AD上的一點,BG,CG分別平分∠ABC,∠ACB,GH⊥BC,垂足為H,求證:查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com