
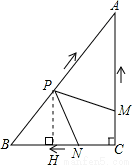
如圖,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.動點M,N從點C同時出發,均以每秒1cm的速度分別沿CA、CB向終點A,B移動,同時動點P從點B出發,以每秒2cm的速度沿BA向終點A移動,連接PM,PN,設移動時間為t(單位:秒,0<t<2.5).
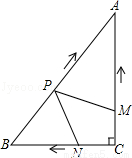
(1)當t為何值時,以A,P,M為頂點的三角形與△ABC相似?
(2)是否存在某一時刻t,使四邊形APNC的面積S有最小值?若存在,求S的最小值;若不存在,請說明理由.
(1)當t=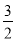 時,以A、P、M為頂點的三角形與△ABC相似;
時,以A、P、M為頂點的三角形與△ABC相似;
(2)當t= 時,四邊形APNC的面積S有最小值,其最小值是
時,四邊形APNC的面積S有最小值,其最小值是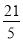
【解析】
試題分析:根據勾股定理求得AB=5cm.
(1)分類討論:△AMP∽△ABC和△APM∽△ABC兩種情況.利用相似三角形的對應邊成比例來求t的值;
(2)如圖,過點P作PH⊥BC于點H,構造平行線PH∥AC,由平行線分線段成比例求得以t表示的PH的值;然后根據“S=S△ABC-S△BPH”列出S與t的關系式S=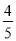 (t-
(t- )2+
)2+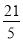 (0<t<2.5),則由二次函數最值的求法即可得到S的最小值.
(0<t<2.5),則由二次函數最值的求法即可得到S的最小值.
試題解析:∵如圖,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.
∴根據勾股定理,得AB=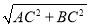 =5cm.
=5cm.
(1)以A,P,M為頂點的三角形與△ABC相似,分兩種情況:
①當△AMP∽△ABC時,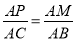 ,
,
即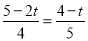 ,
,
解得t=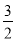 ;
;
②當△APM∽△ABC時,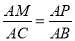 ,
,
即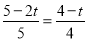 ,
,
解得t=0(不合題意,舍去);
綜上所述,當t=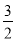 時,以A、P、M為頂點的三角形與△ABC相似;
時,以A、P、M為頂點的三角形與△ABC相似;
(2)存在某一時刻t,使四邊形APNC的面積S有最小值.理由如下:
假設存在某一時刻t,使四邊形APNC的面積S有最小值.
如圖,過點P作PH⊥BC于點H.則PH∥AC,
∴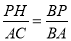 ,
,
即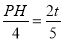 ,
,
∴PH=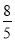 t,
t,
∴S=S△ABC-S△BPN,
=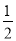 ×3×4-
×3×4-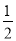 ×(3-t)•
×(3-t)•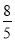 t,
t,
=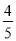 (t-
(t- )2+
)2+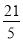 (0<t<2.5).
(0<t<2.5).
∵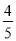 >0,
>0,
∴S有最小值.
當t= 時,S最小值是
時,S最小值是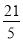 .
.
答:當t= 時,四邊形APNC的面積S有最小值,其最小值是
時,四邊形APNC的面積S有最小值,其最小值是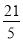 .
.
考點:相似形綜合題.


科目:初中數學 來源:2014-2015學年黑龍江省雞西市八年級上學期期中考試數學試卷(解析版) 題型:選擇題
三條直線相交于同一點時,對頂角有m對,交于不同三點時,對頂角有n對,則m與n的關系是( )
A、m>n B、m=n C、m<n D、m+n=10
查看答案和解析>>
科目:初中數學 來源:2014-2015學年山東省九年級上學期期末模擬考試數學試卷(解析版) 題型:選擇題
6張大小、厚度、顏色相同的卡片上分別畫上線段、等邊三角形、等腰梯形、平行四邊形、五角星、圓.在看不見圖形的條件下任意摸出1張,這張卡片上的圖形是中心對稱圖形的概率是( )
A.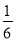 B.
B.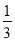 C.
C.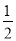 D.
D.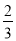
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省啟東市濱海實驗校共同體九年級上學期第二次質檢數學試卷(解析版) 題型:解答題
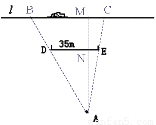
如示意圖,小華家(點A處)和公路(l)之間豎立著一塊35m長且平行于公路的巨型廣告牌(DE).廣告牌擋住了小華的視線,請在圖中畫出視點A的盲區,并將盲區內的那段公路計為BC.一輛以60km/h勻速行駛的汽車經過公路段的時間是3s,已知廣告牌和公路的距離是40m,求小華家到公路的距離.(精確到1m)
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省啟東市濱海實驗校共同體九年級上學期第二次質檢數學試卷(解析版) 題型:填空題
函數 的圖象如下圖所示,則結論:
的圖象如下圖所示,則結論:

①兩函數圖象的交點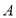 的坐標為
的坐標為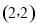 ;
;
②當 時,
時, ;
;
③當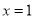 時,
時,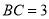 ;
;
④當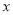 逐漸增大時,
逐漸增大時,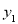 隨著
隨著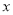 的增大而增大,
的增大而增大,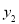 隨著
隨著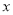 的增大而減小.
的增大而減小.
其中正確結論的序號是 .
查看答案和解析>>
科目:初中數學 來源:2014-2015學年重慶市八年級上學期期末模擬數學試卷(解析版) 題型:解答題
為弘揚中華民族傳統文化,某校舉辦了“古詩文大賽”,并為獲獎同學購買簽字筆和筆記本作為獎品.1支簽字筆和2個筆記本共8.5元,2支簽字筆和3個筆記本共13.5元.
(1)求簽字筆和筆記本的單價分別是多少元?
(2)為了激發學生的學習熱情,學校決定給每名獲獎同學再購買一本文學類圖書,如果給每名獲獎同學都買一本圖書,需要花費720元;書店出臺如下促銷方案:購買圖書總數超過50本可以享受8折優惠.學校如果多買12本,則可以享受優惠且所花錢數與原來相同.問學校獲獎的同學有多少人?
查看答案和解析>>
科目:初中數學 來源:2014-2015學年浙江省八年級上學期期中檢測數學試卷(解析版) 題型:選擇題
如圖,在△ABC中,CF⊥AB于F,BE⊥AC于E,M為BC的中點,EF=5,BC=8,則△EFM的周長是 ( )

A.13 B.18 C.15 D.21
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com