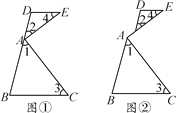
【題目】如圖，∠EAC＝90°，∠1＋∠2＝90°，∠1＝∠3，∠2＝∠4.
(1)如圖①，求證：DE∥BC；
(2)若將圖①改變為圖②，其他條件不變，(1)中的結論是否仍成立？請說明理由．
【答案】見解析
【解析】（1）首先證明∠1+∠3+∠2+∠4=180°，進而證明∠D+∠B=180°，即可解決問題．
（2）如圖，作輔助線，證明∠AEC+∠ACE+∠3+∠4=180°，即可解決問題．
試題解析：（1）如圖1，
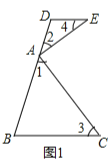
∵∠1=∠3，∠2=∠4，
∴∠1+∠3+∠2+∠4=2（∠1+∠2），
∵∠1+∠2=90°，
∴∠1+∠3+∠2+∠4=180°；
∵∠D+∠B+∠1+∠3+∠2+∠4=360°，
∴∠D+∠B=180°，
∴DE∥BC．
（2）成立．
如圖2，連接EC；
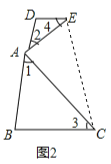
∵∠1=∠3，∠2=∠4，且∠1+∠2=90°，
∴∠3+∠4=∠1+∠2=90°；
∵∠EAC=90°，
∴∠AEC+∠ACE=180°-90°=90°，
∴∠AEC+∠ACE+∠3+∠4=180°，
∴DE∥BC，
即（1）中的結論仍成立．
科目：初中數學 來源： 題型：
【題目】如圖，已知反比例函數y1=
與一次函數y2=k2x+b的圖象交于點A（1，8），B（-4，m）兩點．
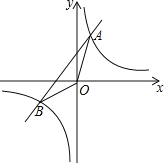
（1）求k1，k2，b的值；
（2）求△AOB的面積；
（3）請直接寫出不等式
x+b的解．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知反比例函數y1=
與一次函數y2=k2x+b的圖象交于點A（1，8），B（-4，m）兩點．
（1）求k1，k2，b的值；
（2）求△AOB的面積；
（3）請直接寫出不等式
x+b的解．
查看答案和解析>>
科目：初中數學 來源： 題型：
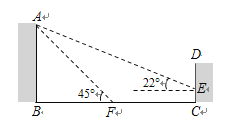
【題目】（滿分8分）如圖，某教學樓AB的后面有一建筑物CD，當光線與地面的夾角是22°時，教學樓在建筑物的墻上留下高2m的影子CE；而當光線與地面的夾角是45°時，教學樓頂A在地面上的影子F與墻角C的距離為18m (B、F、C在一條直線上).
求教學樓AB的高度.（結果保留整數）
（參考數據：sin22°
0.37，cos22°
0.93，tan22°
0.40 .）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】下列事件概率為1的是（ ）
A.射擊運動員射擊一次，命中靶心
B.任意畫一個三角形，其外角和是360°
C.籃球隊員投籃一次未命中
D.丟一個骰子，向上一面的點數為7
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：如圖，在△ABC中，M是邊AB的中點，D是邊BC延長線上的一點，且CD= 
BC，作DN∥CM交AC于點N．求證：四邊形MCDN是平行四邊形．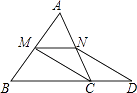 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某航空母艦的滿載排水量為60900噸．將數60900用科學記數法表示為（ ）
A. 0.609×105 B. 6.09×104 C. 60.9×103 D. 609×102
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，正方形ABCD的邊AB在數軸上，數軸上點A表示的數為-1，正方形ABCD的面積為16．
（1）數軸上點B表示的數為 ；
（2）將正方形ABCD沿數軸水平移動，移動后的正方形記為
，移動后的正方形
與原正方形ABCD重疊部分的面積記為S．
① 當S =4時，畫出圖形，并求出數軸上點
表示的數；
② 設正方形ABCD的移動速度為每秒2個單位長度，點E為線段
的中點，點F在線段
上，且
. 經過
秒后，點E，F所表示的數互為相反數，直接寫出
的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
