Question

對x，y定義一種新運算T，規定：T（x，y）=（其中a、b均為非零常數），這里等式右邊是通常的四則運算，例如：T（0，1）==b．

（1）已知T（1，﹣1）=﹣2，T（4，2）=1．

①求a，b的值；

②若關于m的不等式組恰好有3個整數解，求實數p的取值范圍；

（2）若T（x，y）=T（y，x）對任意實數x，y都成立（這里T（x，y）和T（y，x）均有意義），則a，b應滿足怎樣的關系式？

Answer 1

【考點】分式的混合運算；解二元一次方程組；一元一次不等式組的整數解．

【專題】新定義．

【分析】（1）①已知兩對值代入T中計算求出a與b的值；

②根據題中新定義化簡已知不等式，根據不等式組恰好有3個整數解，求出p的范圍即可；

（2）由T（x，y）=T（y，x）列出關系式，整理后即可確定出a與b的關系式．

【解答】解：（1）①根據題意得：T（1，﹣1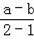）==﹣2，即a﹣b=﹣2；

T=（4，2）==1，即2a+b=5，

解得：a=1，b=3；

②根據題意得：，

由①得：m≥﹣；

由②得：m＜，

∴不等式組的解集為﹣≤m＜，

∵不等式組恰好有3個整數解，即m=0，1，2，

∴2＜≤3，

解得：﹣2≤p＜﹣；

 

（2）由T（x，y）=T（y，x），得到=，

整理得：（x²﹣y²）（2b﹣a）=0，

∵T（x，y）=T（y，x）對任意實數x，y都成立，

∴2b﹣a=0，即a=2b．

【點評】此題考查了分式的混合運算，解二元一次方程組，以及一元一次不等式組的整數解，弄清題中的新定義是解本題的關鍵．