Question

【題目】在平面直角坐標系xOy中，給出如下定義：

對于⊙C及⊙C外一點P，M，N是⊙C上兩點，當∠MPN最大時，稱∠MPN為點P關于⊙C的“視角”．

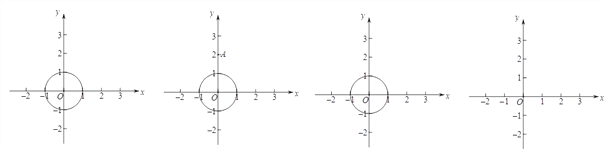
（1）如圖，⊙O的半徑為1，

①已知點A（0，2），畫出點A關于⊙O的“視角”；

若點P在直線x = 2上，則點P關于⊙O的最大“視角”的度數 ；

②在第一象限內有一點B（m，m），點B關于⊙O的“視角”為60°，求點B的坐標；

③若點P在直線上，且點P關于⊙O的“視角”大于60°，求點P的橫坐標的取值范圍．

（2）⊙C的圓心在x軸上，半徑為1，點E的坐標為（0，1），點F的坐標為（0，-1），若線段EF上所有的點關于⊙C的“視角”都小于120°，直接寫出點C的橫坐標的取值范圍．

Answer 1

【答案】（1）①畫圖見解析；②B（， ）③0<<（2）<或>．

【解析】（1）①如圖1中，過點A作⊙O的切線，切點分別為M、N. 點A關于⊙O的“視角”就是兩條切線的夾角，∠MAN就是點P在直線x = 2關于⊙O的“視角”；②由①可知，點A關于⊙O的“視角”為60°，根據對稱性即可推出點B的坐標；由點P在直線上，從而可求出點P的橫坐標的取值范圍.

（2）當⊙C的圓心在x軸上，設切點為P，連接PC則PC⊥AP，想辦法求出點C的坐標，求出此時的點C坐標，即可解決問題.

解：（1）①畫圖

60°

②∵點B關于⊙O的視角為60°，

∴點B在以O為圓心，2為半徑的圓上，即OB=2

∵B（m，m） (m>0)，

∴OB=，

∴.

∴B（， ）

③∵點P關于⊙O的“視角”大于60°，

∴點P在以O為圓心1為半徑與2為半徑的圓環內.

∵點P在直線上，由上可得 =0或

∴0<<

（2）<或>．

“點睛”本題考圓綜合題、切線的性質、一次函數的應用，解題的關鍵是理解題意，靈活應用所學知識解決問題，學會添加常用輔助線，學會尋找特殊位置解決問題，屬于中考壓軸題./span>