
【題目】如圖,優弧![]() 紙片所在
紙片所在![]() 的半徑為2,
的半徑為2,![]() ,點
,點![]() 為優弧
為優弧![]() 上一點(點
上一點(點![]() 不與
不與![]() ,
,![]() 重合),將圖形沿
重合),將圖形沿![]() 折疊,得到點
折疊,得到點![]() 的對稱點
的對稱點![]() .當
.當![]() 與
與![]() 相切時,則折痕
相切時,則折痕![]() 的長
的長![]() ______.
______.
【答案】![]()
【解析】
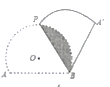
根據切線的性質得到∠OBA′=90°,從而得到∠ABA′=120°,就可求出∠ABP,進而求出∠OBP=30°.過點O作OG⊥BP,垂足為G,容易求出OG、BG的長,根據垂徑定理就可求出折痕的長.
解:過點O作OH⊥AB,垂足為H,連接OB,如圖所示.
∵OH⊥AB,AB=![]() ,
,
∴AH=BH=![]() ,
,
∵OB=2,
∴OH=1.
∴點O到AB的距離為1.過點O作OG⊥BP,垂足為G,如圖所示.
∵BA′與⊙O相切,
∴OB⊥A′B.
∴∠OBA′=90°.
∵∠OBH=30°,
∴∠ABA′=120°.
∴∠A′BP=∠ABP=60°.
∴∠OBP=30°.
∴OG=![]() OB=1.
OB=1.
∴BG=![]()
![]() ,
,
∵OG⊥BP,
∴BG=PG=![]() ,
,
∴BP=![]() ,
,
∴折痕PB的長為![]() ,
,
故答案為:![]() .
.


 全程金卷系列答案
全程金卷系列答案 快樂5加2金卷系列答案
快樂5加2金卷系列答案科目:初中數學 來源: 題型:
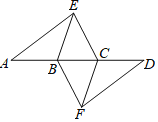
【題目】如圖,點A、B、C、D依次在同一條直線上,點E、F分別在直線AD的兩側,已知BE∥CF,∠A=∠D,AE=DF.
(1)求證:四邊形BFCE是平行四邊形;
(2)填空:若AD=7,AB=2.5,∠EBD=60°,當四邊形BFCE是菱形時,菱形BFCE的面積是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某小區![]() 號樓對外銷售,已知
號樓對外銷售,已知![]() 號樓某單元共
號樓某單元共![]() 層,一樓為商鋪,只租不售,二樓以上價格如下:第
層,一樓為商鋪,只租不售,二樓以上價格如下:第![]() 層售價為
層售價為![]() 元/米
元/米![]() ,從第
,從第![]() 層起每上升一層,每平方米的售價提高
層起每上升一層,每平方米的售價提高![]() 元,反之每降一層,每平方米的售價降低
元,反之每降一層,每平方米的售價降低![]() 元,已知該單元每套的面積均為
元,已知該單元每套的面積均為![]() 米
米![]()
優惠活動
活動一:若一次性付清所有房款,降價![]() ,另免
,另免![]() 年物業費共
年物業費共![]() 元.
元.
活動二:若購買者一次性付清所有房款,降價![]() ,無贈送.
,無贈送.
(1)請在下表中,補充完整售價![]() (元/米
(元/米![]() )與樓層
)與樓層![]() (
(![]() 取正整數)之間的的數關系式.
取正整數)之間的的數關系式.
樓層 |
|
|
|
|
售價 | 不售 |
|
(2)某客戶想購買該單元第![]() 層的一套樓房,若他一次性付清購房款,可以參加如圖優惠活動.請你幫助他分析哪種優惠方案更合算
層的一套樓房,若他一次性付清購房款,可以參加如圖優惠活動.請你幫助他分析哪種優惠方案更合算

查看答案和解析>>
科目:初中數學 來源: 題型:
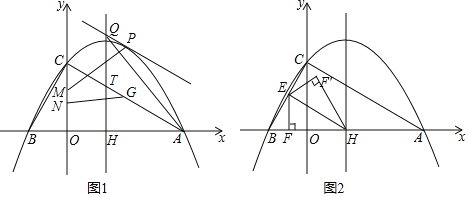
【題目】如圖1,拋物線y![]() 2
2![]() 與x軸相交于A、B兩點(點A在點B的右側),與y軸相交于點C,對稱軸與x軸相交于點H,與AC相交于點T.
與x軸相交于A、B兩點(點A在點B的右側),與y軸相交于點C,對稱軸與x軸相交于點H,與AC相交于點T.
(1)點P是線段AC上方拋物線上一點,過點P作PQ∥AC交拋物線的對稱軸于點Q,當△AQH面積最大時,點M、N在y軸上(點M在點N的上方),MN![]() ,點G在直線AC上,求PM+NG
,點G在直線AC上,求PM+NG![]() GA的最小值.
GA的最小值.
(2)點E為BC中點,EF⊥x軸于F,連接EH,將△EFH沿EH翻折得△EF'H,如圖所示2,再將△EF'H沿直線BC平移,記平移中的△EF'H為△E'F″H',在平移過程中,直線E'H'與x軸交于點R,則是否存在這樣的點R,使得△RF'H'為等腰三角形?若存在,求出R點坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
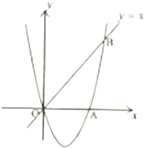
【題目】如圖,經過原點![]() 的拋物線
的拋物線![]() 與
與![]() 軸交于另一點
軸交于另一點![]() ,在第一象限內與直線
,在第一象限內與直線![]() 交于點
交于點![]() .
.
(1)求這條拋物線的解析式;
(2)在第四象限內的拋物線上有一點![]() ,滿足以
,滿足以![]() ,
,![]() ,
,![]() 為頂點的三角形的面積為1,求點
為頂點的三角形的面積為1,求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
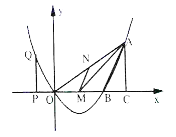
【題目】如圖,二次函數的圖象經過原點![]() 和
和![]() ,與
,與![]() 軸交于另一點
軸交于另一點![]() ,且對稱軸是
,且對稱軸是![]() .
.
(1)求二次函數的表達式;
(2)若![]() 是
是![]() 上的一點,作
上的一點,作![]() ,交
,交![]() 于點
于點![]() ,當
,當![]() 的面積最大時,求點
的面積最大時,求點![]() 的坐標;
的坐標;
(3)![]() 是
是![]() 軸上的點,過
軸上的點,過![]() 作
作![]() 軸,與拋物線交于點
軸,與拋物線交于點![]() ,過
,過![]() 作
作![]() 軸于
軸于![]() ,是否存在點
,是否存在點![]() ,使以點
,使以點![]() 、
、![]() 、
、![]() 為頂點的三角形與以點
為頂點的三角形與以點![]() 、
、![]() 、
、![]() 為頂點的三角形相似?若存在,求出點
為頂點的三角形相似?若存在,求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
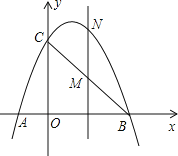
【題目】如圖,已知拋物線經過點A(﹣1,0)、B(3,0)、C(0,3)三點.
(1)求拋物線的解析式.
(2)點M是線段BC上的點(不與B,C重合),過M作MN∥y軸交拋物線于N,若點M的橫坐標為m,請用m的代數式表示MN的長.
(3)在(2)的條件下,連接NB、NC,是否存在m,使△BNC的面積最大?若存在,求m的值;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com