
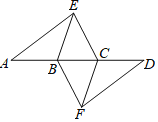
【題目】如圖,點A、B、C、D依次在同一條直線上,點E、F分別在直線AD的兩側,已知BE∥CF,∠A=∠D,AE=DF.
(1)求證:四邊形BFCE是平行四邊形;
(2)填空:若AD=7,AB=2.5,∠EBD=60°,當四邊形BFCE是菱形時,菱形BFCE的面積是 .
【答案】(1)詳見解析;(2)2![]()
【解析】
(1)證明△ABE≌△DCF,繼而得到BE=CF,再結合BE//CF 即可解決問題.
(2)利用全等三角形的性質證明AB=CD,由菱形的性質求出EF的長,即可解決問題.
(1)∵BE∥CF,
∴∠EBC=∠FCB,
∴∠EBA=∠FCD,
在△ABE和△DCF中,
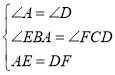 ,
,
∴△ABE≌△DCF(AAS),
∴BE=CF,
又∵BE//CF,
∴四邊形BFCE是平行四邊形;
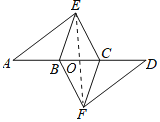
(2)連接EF交BC于O,如圖所示:
∵△ABE≌△DCF,
∴AB=CD,
∵AD=7,AB=DC=2.5,
∴BC=AD﹣AB﹣DC=2,
∵四邊形BFCE是菱形,∠EBD=60°,EF⊥BC,OB=![]() BC=1,OE=OF,
BC=1,OE=OF,
∴△CBE是等邊三角形,∠BEO=30°,
∴BE=BC=2,
∴OE=![]() =
=![]() ,
,
∴EF=2![]() ,
,
∴菱形BFCE的面積=![]() BC×EF=
BC×EF=![]() ×2×2
×2×2![]() =2
=2![]() ,
,
故答案為:2![]() .
.


科目:初中數學 來源: 題型:
【題目】立定跳遠是體育中考選考項目之一,體育課上老師記錄了某同學的一組立定跳遠成績如表:
成績(m) | 2.3 | 2.4 | 2.5 | 2.4 | 2.4 |
則下列關于這組數據的說法,正確的是( )
A.眾數是2.3B.平均數是2.4
C.中位數是2.5D.方差是0.01
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某特產店出售大米,一天可銷售20袋,每袋可盈利40元,為了擴大銷售,增加盈利,盡快減少庫存,決定采取降價措施,據統計發現,若每袋降價2元,平均每天可多售4袋.
(1)設每袋大米降價為x(x為偶數)元時,利潤為y元,寫出y與x的函數關系式.
(2)若每天盈利1200元,則每袋應降價多少元?
(3)每袋大米降價多少元時,商店可獲最大利潤?最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
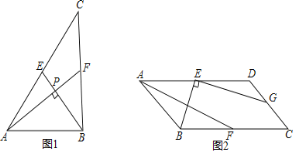
【題目】如圖1,AF,BE是△ABC的中線,AF⊥BE,垂足為點P,設BC=a,AC=b,AB=c,則a2+b2=5c2,利用這一性質計算.如圖2,在平行四邊形ABCD中,E,F,G分別是AD,BC,CD的中點,EB⊥EG于點E,AD=8,AB=2![]() ,則AF=__.
,則AF=__.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩個批發店銷售同一種蘋果.在甲批發店,不論一次購買數量是多少,價格均為6元/kg.在乙批發店,一次購買數量不超過元50kg時,價格為7元/kg;一次購買數量超過50kg時,其中有50kg的價格仍為7元/kg,超出50kg部分的價格為5元/kg.設小王在同一個批發店一次購買蘋果的數量為![]()
![]() .
.
(Ⅰ)根據題意填表:
一次購買數量/kg | 30 | 50 | 150 | … |
甲批發店花費/元 | 300 | … | ||
乙批發店花費/元 | 350 | … |
(Ⅱ)設在甲批發店花費![]() 元,在乙批發店花費
元,在乙批發店花費![]() 元,分別求
元,分別求![]() ,
,![]() 關于
關于![]() 的函數解析式;
的函數解析式;
(Ⅲ)根據題意填空:
①若小王在甲批發店和在乙批發店一次購買蘋果的數量相同,且花費相同,則他在同一個批發店一次購買蘋果的數量為____________kg;
②若小王在同一個批發店一次購買蘋果的數量為120kg,則他在甲、乙兩個批發店中的________批發店購買花費少;
③若小王在同一個批發店一次購買蘋果花費了360元,則他在甲、乙兩個批發店中的________批發店購買數量多.
查看答案和解析>>
科目:初中數學 來源: 題型:
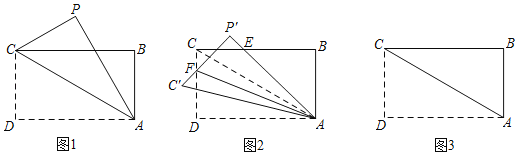
【題目】如圖1,在矩形紙片ABCD中,AB=2![]() ,AD=6,將紙片沿對角線AC對折,點D落在點P處.
,AD=6,將紙片沿對角線AC對折,點D落在點P處.
(1)填空:∠BCA的大小是 ;
(2)如圖2,呂家三少將折疊后的紙片沿著AC剪開,把△APC繞點A逆時針旋轉α角(0°≤α≤90°),得到△AP′C′,點P,C分別對應點P′,C′,P′A交BC于點E,P′C′交CD于點F.
①點α=15時,求證:AB=BE;
②填空:當點P′落在邊BC上時,連接AF,則tan∠DAF的值為 ;
③填空:在②的條件下,將△AP′C′沿著AP′折疊至△AP′C″處,點C′對應點C″,AC″交BC于點G,則線段BG的長度為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四張正面分別寫有1、2、3、4的不透明卡片,它們的背面完全相同,現把它們洗勻,背面朝上放置后,開始游戲![]() 游戲規則如下:
游戲規則如下:
連摸三次,每次隨機摸出一張卡片,并翻開記下卡片上的數字,每次摸出后不放回,如果第三次摸出的卡片上的數字,正好介于第一、二次摸出的卡片上的數字之間,則游戲勝出,否則,游戲失敗![]() 問:
問:
![]() 若已知小明第一次摸出的數字是4,第二次摸出的數字是2,在這種情況下,小明繼續游戲,可以獲勝的概率為______.
若已知小明第一次摸出的數字是4,第二次摸出的數字是2,在這種情況下,小明繼續游戲,可以獲勝的概率為______.
![]() 若已知小明第一次摸出的數字是3,求在這種情況下,小明繼續游戲,可以獲勝的概率
若已知小明第一次摸出的數字是3,求在這種情況下,小明繼續游戲,可以獲勝的概率![]() 要求列表或用樹狀圖求
要求列表或用樹狀圖求![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
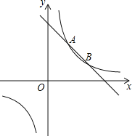
【題目】如圖,反比例函數y=![]() 的圖象和一次函數的圖象交于A、B兩點,點A的橫坐標和點B的縱坐標都是1.
的圖象和一次函數的圖象交于A、B兩點,點A的橫坐標和點B的縱坐標都是1.
(1)在第一象限內,寫出關于x的不等式kx+b≥![]() 的解集 ;
的解集 ;
(2)求一次函數的表達式;
(3)若點P(m,n)在反比例函數圖象上,且關于y軸對稱的點Q恰好落在一次函數的圖象上,求m2+n2的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
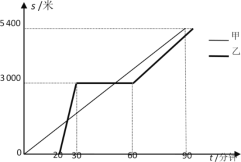
【題目】某景區在同一線路上順次有三個景點A,B,C,甲、乙兩名游客從景點A出發,甲步行到景點C;乙花20分鐘時間排隊后乘觀光車先到景點B,在B處停留一段時間后,再步行到景點C.甲、乙兩人離景點A的路程s(米)關于時間t(分鐘)的函數圖像如圖所示.
(1)甲的速度是 米/分鐘;
(2)當20≤t ≤30時,求乙離景點A的路程s與t的函數表達式;
(3)乙出發后多長時間與甲在途中相遇?
(4)若當甲到達景點C時,乙與景點C的路程為360米,則乙從景點B步行到景點C的速度是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com