
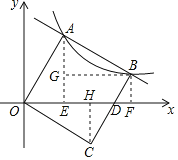
【題目】如圖,平面直角坐標系中,O為坐標原點,正方形OABC的定點A,B都在反比例函數y=![]() (k>0,x>0)的圖象上,邊BC與x軸交于點D,則
(k>0,x>0)的圖象上,邊BC與x軸交于點D,則![]() 的值為( )
的值為( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
過A作AE⊥x軸于E,過B作BF⊥x軸于F,BG⊥AE于G,于是得到EF=BG,BF=GE,根據正方形的性質得到OA=AB,∠OAB=90°,根據余角的性質得到∠OAE=∠ABG,根據全等三角形的性質得到AG=OE,AE=BG,設A(a,![]() ),得到OE=AG=a,AE=BG=
),得到OE=AG=a,AE=BG=![]() ,求得B(
,求得B(![]() +a,
+a,![]() -a),得方程求得k=
-a),得方程求得k=![]() a2(負值舍去),過C作CH⊥x軸于H,根據相似三角形的性質即可得到結論.
a2(負值舍去),過C作CH⊥x軸于H,根據相似三角形的性質即可得到結論.
解:過A作AE⊥x軸于E,過B作BF⊥x軸于F,BG⊥AE于G,
則EF=BG,BF=GE,
∵四邊形OABC是正方形,
∴OA=AB,∠OAB=90°,
∴∠OAE+∠BAE=∠BAE+∠ABG=90°,
∴∠OAE=∠ABG,
在△AOE與△BAG中,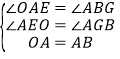 ,
,
∴△AOE≌△BAG,
∴AG=OE,AE=BG,
設A(a,![]() ),
),
∴OE=AG=a,AE=BG=![]() ,
,
∴B(![]() +a,
+a,![]() -a),
-a),
∴(![]() +a)(
+a)(![]() -a)=k,
-a)=k,
解得k=![]() a2(負值舍去),
a2(負值舍去),
∴B點的縱坐標為![]() a,
a,
BF=![]() a,
a,
過C作CH⊥x軸于H,
同理△AOE≌△OCH,
∴CH=OE=a,
∵CH⊥x軸,BF⊥x軸,
∴CH∥BF,
∴△BFD∽△CHD,
∴![]() =
=![]() =
=![]() =
=![]() ,
,
故選:D.


科目:初中數學 來源: 題型:
【題目】如圖是反比例函數y=![]() 的圖象的一個分支,對于給出的下列說法:
的圖象的一個分支,對于給出的下列說法:

①常數k的取值范圍k>2;②另一分支在第三象限;③在函數圖象上取點A(a1,b1)和點B(a2,b2),當a1>a2時,則b1<b2;④在函數圖象的某一分支上取點A(a1,b1)和點B(a2,b2),當a1>a2時,則b1<b2.其中正確的是__________.(在橫線上填上正確的序號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,E是矩形ABCD的邊AD上一點,且BE=ED,P是對角線BD上任一點,PF⊥BE,PG⊥AD,垂足分別為F,G,求證:PF+PG=AB.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,已知![]() 于點D,AE平分
于點D,AE平分![]()
(1)試探究![]() 與
與![]() 的關系;
的關系;
(2)若F是AE上一動點,當F移動到AE之間的位置時,![]() ,如圖2所示,此時
,如圖2所示,此時![]() 的關系如何?
的關系如何?
(3)若F是AE上一動點,當F繼續移動到AE的延長線上時,如圖3,![]() ,①中的結論是否還成立?如果成立請說明理由,如果不成立,寫出新的結論.
,①中的結論是否還成立?如果成立請說明理由,如果不成立,寫出新的結論.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】光明中學全體學生900人參加社會實踐活動,從中隨機抽取50人的社會實踐活動成績制成如圖所示的條形統計圖,結合圖中所給信息解答下列問題:
![]() 填寫下表:
填寫下表:
中位數 | 眾數 | |
隨機抽取的50人的社會實踐活動成績 |
![]() 估計光明中學全體學生社會實踐活動成績的總分.
估計光明中學全體學生社會實踐活動成績的總分.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AD,AE分別是△ABC的高和角平分線,

(1)若∠ABC=30°,∠ACB=50°,求∠DAE的度數
(2)寫出∠DAE與∠C-∠B的數量關系,并證明你的結論
查看答案和解析>>
科目:初中數學 來源: 題型:
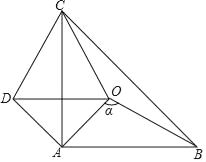
【題目】如圖,△ABC和△AOD是等腰直角三角形,AB=AC,AO=AD,∠BAC=∠OAD=90°,點O是△ABC內的一點,∠BOC=130°.
(1)求證:OB=DC;
(2)求∠DCO的大小;
(3)設∠AOB=α,那么當α為多少度時,△COD是等腰三角形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】先閱讀一段文字,再回答下列問題:
已知在平面內兩點坐標P1(x1,y1),P2(x2,y2),其兩點間距離公式為 ![]() ,同時,當兩點所在的直線在坐標軸上或平行于x軸或垂直于x軸距離公式可簡化成|x2-x1|或|y2-y1|.
,同時,當兩點所在的直線在坐標軸上或平行于x軸或垂直于x軸距離公式可簡化成|x2-x1|或|y2-y1|.
(1)已知A(3,5),B(-2,-1),試求A,B兩點的距離;
(2)已知A、B在平行于y軸的直線上,點A的縱坐標為5,點B的縱坐標為-1,試求A,B兩點的距離.
(3)已知一個三角形各頂點坐標為A(0,6),B(-3,2),C(3,2),你能斷定此三角形的形狀嗎?說明理由。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)畫出△ABC關于y軸的對稱圖形![]() ,其中A、B、C的對應點分別為
,其中A、B、C的對應點分別為![]() ,
,![]() ,
,![]()
(2)![]() = .
= .
(3)畫出以![]() 為腰的等腰△CAD,點D在y軸右側的小正方形的頂點上,且△CAD的面積為6 .
為腰的等腰△CAD,點D在y軸右側的小正方形的頂點上,且△CAD的面積為6 .

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com