
【題目】如圖,在平面直角坐標系中,已知點A(-3,0),B(0,-1),C(0,![]() )三點.
)三點.
(1)求直線AB的解析式.
(2)若點D在直線AB上,且DB=DC,尺規作圖作出點D(保留作圖痕跡),并求出點D的坐標.

 一本好題口算題卡系列答案
一本好題口算題卡系列答案科目:初中數學 來源: 題型:
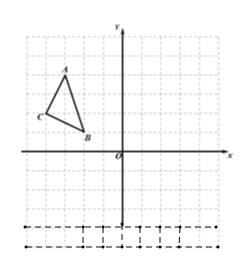
【題目】如圖:在平面直角坐標系中,網格中每一個小正方形的邊長為1個單位長度,△ABC的頂點均在格點上,三個頂點的坐標分別是A(-3,4),B(-2,1),C(-4,2).
(1)將△ABC先向右平移7個單位長度,再向上平移2個單位長度,畫出第二次平移后的△![]() ;
;
(2)以點O(0,0)為對稱中心,畫出與△ABC成中心對稱的△![]() ;
;
(3)將點B繞坐標原點逆時針方向旋轉90°至點![]() ,則點
,則點![]() 的坐標為(______,______)
的坐標為(______,______)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖,點A,B,C,D在一條直線上,填寫下列空格:
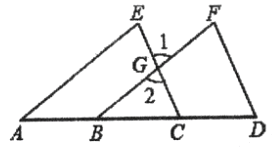
∵AE∥BF(已知)
∴∠E=∠1(______________________)
∵∠E=∠F(已知〉
∴∠_____=∠F(________________)
∴________∥_________(________________________)
查看答案和解析>>
科目:初中數學 來源: 題型:
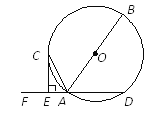
【題目】如圖,AB是⊙O的直徑,AD是⊙O的弦,點F是DA延長線上的一點,過⊙O上一點C作⊙O的切線交DF于點E,CE⊥DF.
(1)求證:AC平分∠FAB;
(2)若AE=1,CE=2,求⊙O的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】現有190張鐵皮做盒子,每張鐵皮可做8個盒身或22個盒底,一個盒身與兩個盒底配成一個完整的盒子,(一張鐵皮只能生產一種產品)
(1)向用多少張鐵皮做盒身,多少張鐵皮做盒底,可以正好用完190張鐵皮并制成一批完整的盒子?
(2)這批盒子一共有多少個?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】問題提出
某商店經銷《超能陸戰隊》超萌“小白”(圖1)玩具,“小白”玩具每個進價60元.為進行促銷,商店制定如下“優惠”方案:如果一次銷售數量不超過10個,則銷售單價為100元/個;如果一次銷售數量超過10個,每增加一個,所有“小白”玩具銷售單價降低1元/個,但單價不得低于80元/個.一次銷售“小白”玩具的單價y(元/個)與銷售數量x(個)之間的函數關系如圖2所示.

(1)求m的值并解釋射線BC所表示的實際意義;
(2)寫出該店當一次銷售x個時,所獲利潤w(元)與x(個)之間的函數關系式;
(3)店長經過一段時間的銷售發現:即并不是銷量越大利潤越大(比如,賣25個賺的錢反而比賣30個賺的錢多).為了不出現這種現象,在其他條件不變的情況下,店長應把原來的最低單價80(元/個)至少提高到多少元/個?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為倡導“低碳生活”,人們常選擇以自行車作為代步工具,如圖是一輛自行車的部分幾何示意圖,其中車架檔AC與CD的長分別為45 cm和60 cm,且它們互相垂直,座桿CE的長為20 cm,點A,C,E在同一條直線上,且∠CAB=75°.(參考數據:sin 75°≈0.966,cos 75°≈0.259,tan 75°≈3.732)
(1)求車架檔AD的長;
(2)求車座點E到車架檔AB的距離(結果精確到1 cm).
查看答案和解析>>
科目:初中數學 來源: 題型:
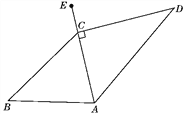
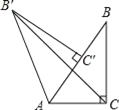
【題目】如圖,在Rt△ABC中,∠ACB=90°,∠BAC=60°,AB=2.Rt△AB′C′可以看作是由Rt△ABC繞A點逆時針方向旋轉60°得到的,求線段 B′C的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com