

分析 (1)根據函數值相等的兩點關于對稱軸對稱,可得B點坐標,根據待定系數法,可得函數解析式;根據自變量與函數值的對應關系,可得C點坐標;
(2)根據等腰三角形的定義,可得關于m的方程,根據解方程,可得m,根據自變量與函數值的對應關系,可得P點坐標;
(3)根據平行于y軸的直線上兩點間的距離是較大的縱坐標減較小的縱坐標,可得EF的長,根據面積的和差,可得二次函數,根據二次函數的性質,可得m的值,面積的最大值;根據自變量與函數值的對應關系,可得E點坐標.
解答 解:(1)由頂點坐標為($\frac{3}{2}$,-$\frac{25}{4}$),得對稱軸為x=$\frac{3}{2}$.
由A、B關于對稱軸對稱,得
$\frac{3}{2}$-(-1)=$\frac{5}{2}$,$\frac{3}{2}$+$\frac{5}{2}$=4,即B點坐標為(4,0).
將A、B、頂點坐標代入函數解析式,得
$\left\{\begin{array}{l}{a-b+c=0}\\{16a+4b+c=0}\\{\frac{9}{4}a+\frac{3}{2}b+4c=-\frac{25}{4}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=1}\\{b=-3}\\{c=-4}\end{array}\right.$,
拋物線的解析式為y=x2-3x-4;
當x=0時,y=-4,即C點坐標為(0,-4);
(2)如圖1: ,
,
設BC的解析式為y=kx+b,將B、C點坐標代入,得
$\left\{\begin{array}{l}{4k+b=0}\\{b=-4}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=1}\\{b=-4}\end{array}\right.$,
BC的解析式為y=x-4,
P在BC上,設P(m,m-4),OP2=m2+(m-4)2,PD2=(m-2)2+(m-4)2,OD2=4.
當PO=OD時,m2+(m-4)2=4化簡,得m2-4m+6=0,方程無解;
當PO=PD時,m2+(m-4)2=(m-2)2+(m-4)2,化簡,得4m-4=0,解得m=1,m-4=-3,即P(1,-3);
當OD=PD時,(m-2)2+(m-4)2=4,化簡,得m2-6m+8=0,解得m=2,m=4(不符合題意,舍),m-4=-2,即P(2,-2);
綜上所述:當三角形ODP為等腰三角形時,點P的坐標(1,-3),(2,-2);
(3)如圖2: ,
,
E在拋物線上,F在BC上,設E(m,m2-3m-4),F(m,m-4),
EF=m-4-(m2-3m-4)=-m2+4m=-(m-2)2+4,
S△BCE=S△BEF+S△CEF
=$\frac{1}{2}$FE•BH+$\frac{1}{2}$EF•O
H=$\frac{1}{2}$EF•OB
=$\frac{1}{2}$[-(m-2)2+4]×4
當m=2時,S最大=8,
當m=2時,m-4=2-4=-2,即E(2,-2).
點評 本題考查了二次函數綜合題,利用函數值相等的兩點關于對稱軸對稱得出B點坐標是解題關鍵;利用等腰三角形的定義得出關于m的方程式解題關鍵,要分類討論,以防遺漏;利用三角形的面積的和差得出二次函數是解題關鍵.


 暑假作業暑假快樂練西安出版社系列答案
暑假作業暑假快樂練西安出版社系列答案 新活力總動員暑系列答案
新活力總動員暑系列答案科目:初中數學 來源: 題型:選擇題
 如圖,?ABCD中,E是BC邊上一點,BE:EC=1:2,AE交BD于點F,則BF:FD等于( )
如圖,?ABCD中,E是BC邊上一點,BE:EC=1:2,AE交BD于點F,則BF:FD等于( )| A. | 5:7 | B. | 3:5 | C. | 1:3 | D. | 2:5 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
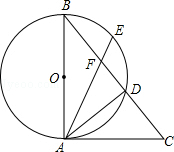 如圖,AB是⊙O的直徑,∠B=∠CAD.
如圖,AB是⊙O的直徑,∠B=∠CAD.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,點O為弧AB所在圓的圓心,OA⊥OB,點P在弧AB上,AP的延長線與OB的延長線交于點C,過點C作CD⊥OP于D.若OP=3,PD=1,則OC=3$\sqrt{2}$.
如圖,點O為弧AB所在圓的圓心,OA⊥OB,點P在弧AB上,AP的延長線與OB的延長線交于點C,過點C作CD⊥OP于D.若OP=3,PD=1,則OC=3$\sqrt{2}$.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖是“北大西洋公約組織”標志的主體部分(平面圖),它是由四邊形OABC繞點O進行3次旋轉變換后形成的.測得AB=BC,OA=OC,∠ABC=40°,則∠OAB的度數是95°.
如圖是“北大西洋公約組織”標志的主體部分(平面圖),它是由四邊形OABC繞點O進行3次旋轉變換后形成的.測得AB=BC,OA=OC,∠ABC=40°,則∠OAB的度數是95°.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 二次函數y=2$\sqrt{3}$x2的圖象如圖,點O為坐標原點,點A在y軸的正半軸上,點B、C在二次函數y=2$\sqrt{3}$x2的圖象上,四邊形OBAC為菱形,且∠OBA=120°,則菱形OBAC的面積是$\frac{9\sqrt{3}}{2}$.
二次函數y=2$\sqrt{3}$x2的圖象如圖,點O為坐標原點,點A在y軸的正半軸上,點B、C在二次函數y=2$\sqrt{3}$x2的圖象上,四邊形OBAC為菱形,且∠OBA=120°,則菱形OBAC的面積是$\frac{9\sqrt{3}}{2}$.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com