
分析 (1)根據一元二次方程x2-3x+k=0有兩個不相等的實數根可得△=(-3)2-4k>0,求出k的取值范圍即可;
(2)根據k的取值范圍,結合k為正整數,得到k的值,進而求出方程的根.
解答 解:(1)∵關于x的一元二次方程x2-3x+k=0有兩個不相等的實數根,
∴△>0,即△=9-4k>0,
∴k<$\frac{9}{4}$;
(2)∵由(1)可知k<$\frac{9}{4}$,
∴選擇k等于2代入原方程得:x2-3x+2=0,
解方程得:x1=2,x2=1.
點評 此題考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c為常數)根的判別式.當△>0,方程有兩個不相等的實數根;當△=0,方程有兩個相等的實數根;當△<0,方程沒有實數根.


科目:初中數學 來源: 題型:選擇題
| A. | (x-2)2=1 | B. | (x+2)2=4 | C. | (x-2)2=-1 | D. | (x-2)2=3 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 錄入漢字個數/人 | 132 | 133 | 134 | 135 | 136 | 137 |
| 甲班參賽學生/人 | 1 | 0 | 1 | 5 | 2 | 1 |
| 乙班參賽學生/人 | 0 | 1 | 4 | 1 | 2 | 2 |
| 平均數 | 中位數 | 眾數 | 方差 | |
| 甲班 | 135 | 135 | 135 | 1.6 |
| 乙班 | 135 | 134.5 | 134 | 1.8 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 3a+6b=9ab | B. | $\frac{1}{2}$y2-$\frac{1}{3}$y2=$\frac{1}{6}$ | C. | 8a4-6a3=2a | D. | 3a3b-3ba3=0 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
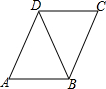 如圖所示,△ABD≌△CDB,下面四個結論中,不正確的是( )
如圖所示,△ABD≌△CDB,下面四個結論中,不正確的是( )| A. | △ABD和△CDB的面積相等 | B. | △ABD和△CDB的周長相等 | ||
| C. | AD∥BC,且AD=BC | D. | ∠A+∠ABD=∠C+∠CBD |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
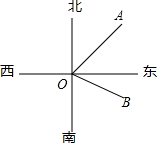 如圖,在燈塔O處觀測到輪船A位于東北方向,同時輪船B在南偏東55°方向,那么∠AOB的大小為( )
如圖,在燈塔O處觀測到輪船A位于東北方向,同時輪船B在南偏東55°方向,那么∠AOB的大小為( )| A. | 80° | B. | 90° | C. | 100° | D. | 85° |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com