
【題目】為了減少霧霾的侵狀,某市環保局與市委各部門協商,要求市民在春節期間禁止燃放煙花爆竹,為了征集市民對禁燃的意見,政府辦公室進行了抽樣調查,調查意見表設計為:“滿意““一般””無所謂””反對”四個選項,調查結果匯總制成如下不完整的統計圖,請根據提供的信息解答下面的問題.
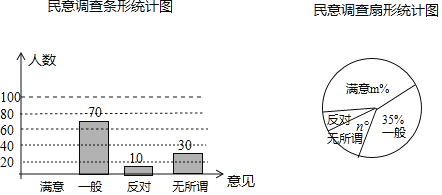
(1)參與問卷調查的人數為 .
(2)扇形統計圖中的m= ,n= .補全條形統計圖;
(3)若本市春節期間留守市區的市民有32000人,請你估計他們中持“反對”意見的人數.
【答案】(1)200;(2)45,15,補圖見解析;(3)本市春節期間留守市民中持“反對”意見的約有1600人.
【解析】
(1)根據持“一般”意見的人數除以其所占的百分比,可得答案;
(2)用調查的總人數減去持“一般”“無所謂”“反對”三個選項的人數得到持“滿意”意見的人數,補全條形圖,用持“滿意”意見的人數除以總人數求出m;用持“無所謂”意見的人數除以總人數求出n;
(3)用本市春節期間留守市區的市民乘以樣本中持“反對”意見的人數所占的百分比,可得答案.
(1)70÷35%=200(人).
故答案為200人;
(2)持“滿意”意見的人數為:200﹣70﹣10﹣30=90(人).
補充條形統計圖如圖所示:
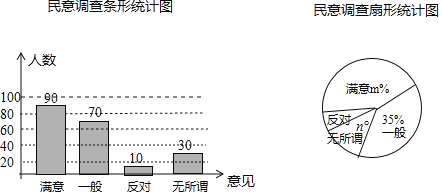
m%=![]() =45%,n%=
=45%,n%=![]() =15%,
=15%,
則m=45,n=15.
故答案為45;15;
(3)樣本中持“反對”意見的有10人,所占百分比為10÷200×100%=5%,
5%×32000=1600(人).
答:本市春節期間留守市民中持“反對”意見的約有1600人.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】取三張形狀大小一樣,質地完全的相同卡片,在三張卡片上分別寫上“李明、王強、孫偉”這三個同學的名字,然后將三張卡片放入一個不透明的盒子里.
(1)林老師從盒子中任取一張,求取到寫有李明名字的卡片概率是多少?
(2)林老師從盒子中取出一張卡片,記下名字后放回,再從盒子中取出第二張卡片,記下名字.用列表或畫樹形圖列出林老師取到的卡片的所有可能情況,并求出兩次都取到寫有李明名字的卡片的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=![]() x2+
x2+![]() x﹣4與x軸交于A、B兩點(點A在點B的左側),與y軸交于點C.
x﹣4與x軸交于A、B兩點(點A在點B的左側),與y軸交于點C.
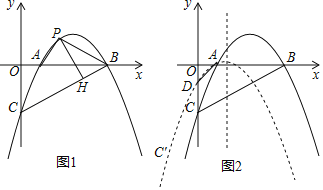
(1)連接BC,P是線段BC上方拋物線上的一動點,過點P作PH⊥BC于點H,當PH長度最大時,在△APB內部有一點M,連接AM、BM、PM,求AM+![]() BM+PM的最小值.
BM+PM的最小值.
(2)若點D是OC的中點,將拋物線y=![]() x2+
x2+![]() x﹣4沿射線AD方向平移
x﹣4沿射線AD方向平移![]() 個單位得到新拋物線y′,C′是拋物線y′上與C對應的點,拋物線y'的對稱軸上有一動點N,在平面直角坐標系中是否存在一點S,使得C′、N、B、S為頂點的四邊形是矩形?若存在,請直接寫出點S的坐標;若不存在,請說明理由.
個單位得到新拋物線y′,C′是拋物線y′上與C對應的點,拋物線y'的對稱軸上有一動點N,在平面直角坐標系中是否存在一點S,使得C′、N、B、S為頂點的四邊形是矩形?若存在,請直接寫出點S的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數![]() 的圖像與二次函數
的圖像與二次函數![]() 的圖像交于
的圖像交于![]() 、
、![]() 兩點,點
兩點,點![]() 在
在![]() 軸上,點
軸上,點![]() 的橫坐標為4.
的橫坐標為4.
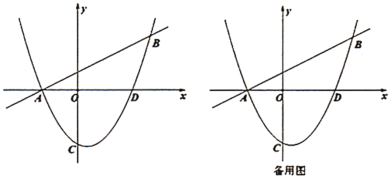
(1)![]() ________,
________,![]() ________;
________;
(2)設二次函數的圖像與![]() 軸交于
軸交于![]() 點,與
點,與![]() 軸的另一個交點為
軸的另一個交點為![]() ,連接
,連接![]() 、
、![]() ,求
,求![]() 的正弦值;
的正弦值;
(3)①若![]() 點在
點在![]() 軸下方二次函數圖像上,過
軸下方二次函數圖像上,過![]() 點作
點作![]() 軸平行線交直線
軸平行線交直線![]() 于點
于點![]() ,以
,以![]() 點為圓心,
點為圓心,![]() 的長為半徑畫圓,求
的長為半徑畫圓,求![]() 在直線
在直線![]() 上截得的弦長的最大值.
上截得的弦長的最大值.
②若∠ABM=∠ACO,則點M的坐標為_________
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線![]() 與雙曲線
與雙曲線![]() 交于C、D兩點,與x軸交于點A.
交于C、D兩點,與x軸交于點A.
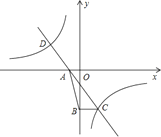
(1)求n的取值范圍和點A的坐標;
(2)過點C作CB⊥y軸,垂足為B,若S△ABC=4,求雙曲線的解析式;
(3)在(1)、(2)的條件下,若AB=![]() ,求點C和點D的坐標并根據圖象直接寫出反比例函數的值小于一次函數的值時,自變量x的取值范圍.
,求點C和點D的坐標并根據圖象直接寫出反比例函數的值小于一次函數的值時,自變量x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】國家規定,中小學生每天在校體育活動時間不低于1小時.為了解這項政策的落實情況,有關部門就“你某天在校體育活動時間是多少”的問題,在某校隨機抽查了部分學生,再根據活動時間![]() (小時)進行分組(A組:
(小時)進行分組(A組:![]() ,B組:
,B組:![]() ,C組:
,C組:![]() ,D組:
,D組:![]() ),繪制成如下兩幅統計圖,請根據圖中信息回答問題:
),繪制成如下兩幅統計圖,請根據圖中信息回答問題:
(1)此次抽查的學生數為________人;
(2)補全條形統計圖;

(3)從抽查的學生中隨機詢問一名學生,該生當天在校體育活動時間低于1小時的概率是__________;
(4)若當天在校學生數為1200人,請估計在當天達到國家規定體育活動時間的學生有__________人.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形![]() 中,
中,![]() 的頂點
的頂點![]() ,
,![]() 分別在
分別在![]() ,
,![]() 邊上,高
邊上,高![]() 與正方形的邊長相等,連接
與正方形的邊長相等,連接![]() 分別交
分別交![]() ,
,![]() 于點
于點![]() ,
,![]() ,下列說法:①
,下列說法:①![]() ;②連接
;②連接![]() ,
,![]() ,則
,則![]() 為直角三角形;③
為直角三角形;③![]() ;④若
;④若![]() ,
,![]() ,則
,則![]() 的長為
的長為![]() ,其中正確結論的個數是( )
,其中正確結論的個數是( )
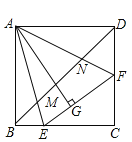
A.4B.3C.2D.1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,直線![]() 交坐標軸于A、C兩點,拋物線
交坐標軸于A、C兩點,拋物線![]() 過A、C兩點.
過A、C兩點.
(1)求拋物線的解析式;
(2)若點P為拋物線位于第三象限上一動點,連接PA,PC,試問△PAC是否存在最大值,若存在,請求出△APC取最大值以及點P的坐標,若不存在,請說明理由;
(3)點M為拋物線上一點,點N為拋物線對稱軸上一點,若△NMC是以∠NMC為直角的等腰直角三角形,請直接寫出點M的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】家住重慶兩相鄰小區的小明和小華在一次數學課后,進行了一次數學實踐活動.如圖,在同一水平面從左往右依次是小明家所在的居民樓、小華家所在的小洋房、背靠小華家的一座小山,實踐內容為測量小山的高度,家住頂樓的小明在窗戶A處測得小山山頂的一棵大樹頂端E的俯角為10°,小華在自家樓下C處測得小明家窗戶A處的仰角為37°,且測得坡面CD的坡度i=1:2,已知兩家水平距離BC=120米,大樹高度DE=3米,則小山山頂D到水平面BF的垂直高度約為( )(精確到0.1米,參考數據sin37°≈![]() ,tan37°≈
,tan37°≈![]() ,sin10°≈
,sin10°≈![]() ,tan10°≈
,tan10°≈![]() )
)

A.55.0米B.50.3米C.48.1 米D.57.3米
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com