
【題目】如圖所示,在![]() 中,
中,![]() ,
,![]() ,
,![]() 為
為![]() 邊上的中點,
邊上的中點,![]() 于點
于點![]() ,
,![]() 交
交![]() 的延長線于點
的延長線于點![]() .
.
(1)求證:![]() ;
;
(2)求證:![]() 垂直平分
垂直平分![]() .
.

【答案】(1)見詳解;(2)見詳解
【解析】
(1)根據ASA判定△ACD≌△CBF即可;
(2)由(1)得到BF=CD,由D為BC中點,根據中點定義得到CD=BD,等量代換得到BF=BD,再根據角度之間的數量關系求出∠ABC=∠ABF,即BA是∠FBD的平分線,從而利用等腰三角形三線合一的性質求證即可.
解:(1)∵∠BCE+∠ACE=90°,∠ACE+∠CAE=90°,
∴∠BCE=∠CAE.
∵AC⊥BC,BF∥AC.
∴BF⊥BC.
∴∠ACD=∠CBF=90°,
∵AC=CB,
∴△ACD≌△CBF;
(2)連接DF,
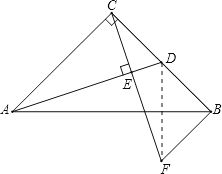
由(1)得CD=BF
∵![]() 為
為![]() 邊上的中點
邊上的中點
∴CD=BD=![]() BC
BC
∴BF=BD
∴△BFD為等腰直角三角形
∵∠ACB=90°,CA=CB,
∴∠ABC=45°.
∵∠FBD=90°,
∴∠ABF=45°.
∴∠ABC=∠ABF,即BA是∠FBD的平分線.
∴根據等腰三角形三線合一的性質有BA⊥FD,BA平分邊FD,
即AB垂直平分DF.


 應用題作業本系列答案
應用題作業本系列答案科目:初中數學 來源: 題型:
【題目】如圖1,在等腰![]() 中,
中,![]() ,點
,點![]() 為邊
為邊![]() 上一點(不與點
上一點(不與點![]() 、點
、點![]() 重合),
重合),![]() ,垂足為
,垂足為![]() ,交
,交![]() 于點
于點![]() .
.
(1)請猜想![]() 與
與![]() 之間的數量關系,并證明;
之間的數量關系,并證明;
(2)若點![]() 為邊
為邊![]() 延長線上一點,
延長線上一點,![]() ,垂足為
,垂足為![]() ,交
,交![]() 延長線于點
延長線于點![]() ,請在圖2中畫出圖形,并判斷(1)中的結論是否成立.若成立,請證明;若不成立,請寫出你的猜想并證明.
,請在圖2中畫出圖形,并判斷(1)中的結論是否成立.若成立,請證明;若不成立,請寫出你的猜想并證明.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形 ABCD 的對角線 AC 與 BD 相交于點 O,CE∥BD, DE∥AC , AD=2![]() , DE=2,則四邊形 OCED 的面積為( )
, DE=2,則四邊形 OCED 的面積為( )

A. 2![]() B. 4 C. 4
B. 4 C. 4![]() D. 8
D. 8
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】從邊長為a的正方形中剪掉一個邊長為b的正方形(如圖1),然后將剩余部分拼成一個長方形(如圖2).
(1)上述操作能驗證的等式是________(填A或B或C)
A.a2-2ab+b2=(a-b)2
B.a2-b2=(a+b)(a-b)
C.a2+ab=a(a+b)
(2)應用你從(1)中選出的等式,完成下列各題:
①已知x2-4y2=12,x+2y=4,求x-2y的值
②計算:(1-![]() )(1-
)(1-![]() )(1-
)(1-![]() )…(1-
)…(1-![]() )(1-
)(1-![]() )
)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校八年級同學到距學校6千米的郊外秋游,一部分同學步行,另一部分同學騎自行車,沿相同路線前往,如圖![]() 分別表示步行和騎車的同學前往目的地所走的路程y(千米)與所用時間
分別表示步行和騎車的同學前往目的地所走的路程y(千米)與所用時間![]() (分鐘)之間的函數關系,則以下判斷錯誤的是 ( )
(分鐘)之間的函數關系,則以下判斷錯誤的是 ( )

A.騎車的同學比步行的同學晚出發30分鐘
B.騎車的同學比步行的同學早6分鐘到達目的地
C.騎車的同學從出發到追上步行的同學用了20分鐘
D.步行同學的速度是6千米/小時,騎車同學的速度是![]() 千米/小時.
千米/小時.
查看答案和解析>>
科目:初中數學 來源: 題型:
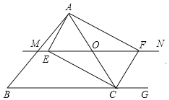
【題目】如圖,![]() 中,點
中,點![]() 是
是![]() 邊上的一個動點,過點
邊上的一個動點,過點![]() 作直線
作直線![]() ,交
,交![]() 的平分線于點
的平分線于點![]() ,交
,交![]() 的外角平分線于點
的外角平分線于點![]() .
.
![]() 判斷
判斷![]() 與
與![]() 的大小關系?并說明理由;
的大小關系?并說明理由;
![]() 當點
當點![]() 運動到何處時,四邊形
運動到何處時,四邊形![]() 是矩形?并說出你的理由;
是矩形?并說出你的理由;
![]() 在
在![]() 的條件下,當
的條件下,當![]() 滿足什么條件時,四邊形
滿足什么條件時,四邊形![]() 是正方形.直接寫出答案,不需說明理由.
是正方形.直接寫出答案,不需說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,是我國第24~30屆奧運獎牌數的回眸和中國代表團獎牌總數統計圖,根據表和統計圖,以下描述正確的是( )
金牌(塊) | 銀牌(塊) | 銅牌(塊) | 總計獎牌數 | |
24 | 5 | 11 | 12 | 28 |
25 | 16 | 22 | 12 | 54 |
26 | 16 | 22 | 12 | 50 |
27 | 28 | 16 | 15 | 59 |
28 | 32 | 17 | 14 | 63 |
29 | 51 | 21 | 28 | 100 |
30 | 38 | 27 | 23 | 88 |

A.中國代表團的奧運獎牌總數一直保持上升趨勢
B.折線統計圖中的六條線段只是為了便于觀察圖象所反映的變化,不表示某種意思
C.與第29屆北京奧運會相比,奧運金牌數、銀牌數、銅牌數都有所下降
D.評價一個代表團在一屆奧運會上的表現,我們只需關注金牌數,無需考慮其他
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com