求下列不定方程的整數解:
(1)72x+157y=1;
(2)9x+21y=144;
(3)103x-91y=5.
解:(1)由原方程得x=
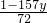
=

①,
∵原方程的解為整數,
∴當y=-11時,x=24,是原方程的一組解,故y=72t-11,代入①式得x=24-157t(t為整數),
故原方程的解為

(t為整數).
(2)由原方程得:x=
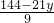
=16-2y-

y①,
∵方程的解整數,16-2是整數,
∴滿足

是整數即可,令

y=t(t為整數),則y=3t,代入①式得,x=16-7t.
故原方程的解為

(t為整數).
(3)由原方程得x=
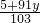
=

①,
∵原方程的解為整數,
∴當y=9時,x=8,是原方程的一組解,
故y=103t+9,代入①式得x=91t+8(t為整數),
原方程的解為

(t為整數).
分析:首先將方程做適當變形,根據解為整數確定其中一個未知數的取值,再進一步求得方程的另一個解.
點評:本題是求不定方程的整數解,先將方程做適當變形,然后列舉出其中一個未知數的適合條件的所有整數值,再求出另一個未知數的值.

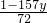 =
= ①,
①, (t為整數).
(t為整數).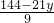 =16-2y-
=16-2y- y①,
y①, 是整數即可,令
是整數即可,令 y=t(t為整數),則y=3t,代入①式得,x=16-7t.
y=t(t為整數),則y=3t,代入①式得,x=16-7t. (t為整數).
(t為整數).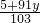 =
= ①,
①, (t為整數).
(t為整數).

 名校課堂系列答案
名校課堂系列答案