
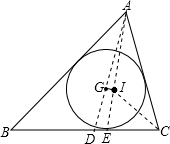
 如圖所示,已知△ABC的重心G與內心I的連線GI∥BC.求證:AB、BC、CA成等差數列.
如圖所示,已知△ABC的重心G與內心I的連線GI∥BC.求證:AB、BC、CA成等差數列.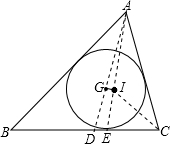 證明:
證明: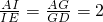 .
.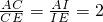 ,即AC=2CE,
,即AC=2CE,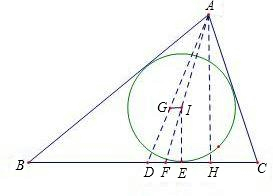
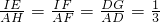 ,即AH=3r.
,即AH=3r.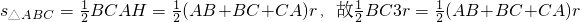 ,
,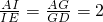 .在△CAE中,利用相似三角形的性質定理易得到
.在△CAE中,利用相似三角形的性質定理易得到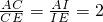 ,即AC=2CE.同理AB=2BE.
,即AC=2CE.同理AB=2BE.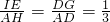 ,即AH=3r.再利用三角形的面積計算公式
,即AH=3r.再利用三角形的面積計算公式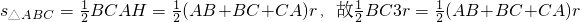 ,即2BC=AB+CA.問題得證.
,即2BC=AB+CA.問題得證.

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com