Question

．如圖，馬路的兩邊CF，DE互相平行，線段CD為人行橫道，馬路兩側的A，B兩點分別表示車站和超市．CD與AB所在直線互相平行，且都與馬路的兩邊垂直，馬路寬20米，A，B相距62米，∠A=67°，∠B=37°．

（1）求CD與AB之間的距離；

（2）某人從車站A出發，沿折線A→D→C→B去超市B．求他沿折線A→D→C→B到達超市比直接橫穿馬路多走多少米．

（參考數據：sin67°≈，cos67°≈，tan6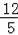7°≈，sin37°≈，cos37°≈，tan37°≈）

Answer 1

【考點】解直角三角形的應用．

【分析】（1）設CD與AB之間的距離為x，則在Rt△BCF和Rt△ADE中分別用x表示BF，AE，又AB=AE+EF+FB，代入即可求得x的值；

（2）在Rt△BCF和Rt△ADE中，分別求出BC、AD的長度，求出AD+DC+CB﹣AB的值即可求解．

【解答】解：（1）CD與AB之間的距離為x，

則在Rt△BCF和Rt△ADE中，

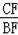
∵=tan3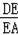7°，=tan67°，

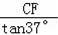
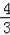
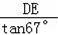
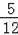
∴BF=≈x，AE=≈x，

又∵AB=62，CD=20，

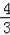
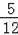
∴x+x+20=62，

解得：x=24，

答：CD與AB之間的距離約為24米；

（2）在Rt△BCF和Rt△ADE中，

∵BC=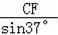≈=40，

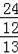
AD=≈=26，

∴AD+DC+CB﹣AB=40+20+26﹣62=24（米），

答：他沿折線A→D→C→B到達超市比直接橫穿馬路多走約24米．