
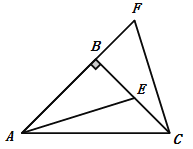
【題目】如圖,在△ABC中,AB=BC, ∠ABC=90°,F為AB 延長線上的一點,點E在BC上,且AE=CF.
(1)求證: △ABE≌△CBF.
(2)若∠CAE=15°,求∠ACF的度數.
【答案】(1)證明見解析;(2)75°
【解析】試題分析:(1)根據“HL”即可判定:△ABE≌△CBF;
(2)由等腰直角三角形的性質得到∠BCA=45°,再由∠CAE=15°,得到∠BAE=30°,由全等三角形的性質得到∠BCF的度數,即可得到結論.
試題解析:(1)證明:∵∠ABC=90°,∴△ABE與△CBF為直角三角形.
在Rt△ABE與Rt△ BCF中,∵AB=BC,AE=CF,∴Rt△ABE≌Rt△ BCF;
(2) ∵ AB=BC, ∠ABC=90°,∴∠BCA=∠BAC=45°.
∵∠CAE=15°,∴∠BAE=30°.
∵△ABE≌△CBF,∴∠BCF=∠BAE=30°,∴∠ACF=75°.


 高效智能課時作業系列答案
高效智能課時作業系列答案科目:初中數學 來源: 題型:
【題目】甲、乙兩人在相同條件下各射靶10次,每次射靶的成績情況如圖所示:
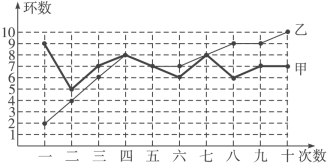
(1)請填寫下表:
平均數 | 方差 | 中位數 | 命中9環及以上的次數 | |
甲 | 7 | 1.2 | 1 | |
乙 | 5.4 |
(2)請從下列四個不同的角度對這次測試結果進行分析:
①從平均數和方差相結合看;
②從平均數和中位數相結合看(分析誰的成績好些);
③從平均數和命中9環以上的次數相結合看(分析誰的成績好些);
④從折線圖上兩人射擊命中環數的走勢看(分析誰更有潛力).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點A,B,C表示某公司三個車間的位置,現在要建一個倉庫,要求它到三個車間的距離相等,則倉庫應建在( )
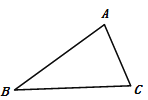
A. △ABC三邊的中線的交點上 B. △ABC三內角平分線的交點上
C. △ABC三內高線的交點上 D. △ABC三邊垂直平分線的交點上
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】用簡便方法計算,將98×102變形正確的是( )
A. 98×102=1002+22B. 98×102=(100﹣2)2
C. 98×102=1002﹣22D. 98×102=(100+2)2
查看答案和解析>>
科目:初中數學 來源: 題型:
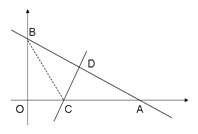
【題目】如圖:一次函數y=-![]() x+6的圖象與x軸和y軸分別交于點A和B ,再將△ AOB沿直線CD對折,使點A與點B重合。直線CD與x軸交于點C,與AB交于點D.
x+6的圖象與x軸和y軸分別交于點A和B ,再將△ AOB沿直線CD對折,使點A與點B重合。直線CD與x軸交于點C,與AB交于點D.
(1)點A的坐標為 ,點B的坐標為 。
(2)求OC的長度 ;
(3)在x軸上有一點P,且△PAB是等腰三角形,不需計算過程,直接寫出點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2010年4月14日上午7時49分,我國青海省玉樹藏族自治州玉樹縣發生里氏7.1級的強烈地震,地震造成重大人員傷亡和財產損失.“地震無情,人間有愛”,某慈善機構將募捐得到的兩批物資第一時間迅速運往災區,第一批共480噸,用8節火車皮和20輛汽車正好裝完;第二批共524噸,用10節火車皮和6輛汽車正好裝完,求每節火車皮和每輛汽車平均各裝多少噸?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com