
【題目】如圖,拋物線與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于
軸交于![]() 、
、![]() 兩點,其中
兩點,其中![]() 、
、![]() 是方程的
是方程的![]() 兩根,且
兩根,且![]() .
.
(![]() )求拋物線的解析式;
)求拋物線的解析式;
(![]() )直線
)直線![]() 上是否存在點
上是否存在點![]() ,使
,使![]() 為直角三角形.若存在,求所有
為直角三角形.若存在,求所有![]() 點坐標;反之說理;
點坐標;反之說理;
(![]() )點
)點![]() 為
為![]() 軸上方的拋物線上的一個動點(
軸上方的拋物線上的一個動點(![]() 點除外),連
點除外),連![]() 、
、![]() ,若設
,若設![]() 的面積為
的面積為![]() .
. ![]() 點橫坐標為
點橫坐標為![]() ,則
,則![]() 在何范圍內時,相應的點
在何范圍內時,相應的點![]() 有且只有
有且只有![]() 個.
個.

【答案】(![]() )
)![]() ;(
;(![]() )
)![]() ;(3)
;(3)![]() .
.
【解析】試題分析:(1)解方程求得拋物線與x軸交點的橫坐標,再用待定系數法求拋物線的解析式即可;(2)用待定系數法求得直線AC的解析式,再分①∠DBC=90°、②∠DBC=90°兩種情況求點D的坐標即可;(3)求得點P在拋物線AB段上時S的最大值,再求得點P在拋物線AC段上時,S的最大值,即可得S的取值范圍.
試題解析:
(![]() )
)![]() ,
,
![]() ,
, ![]() ,
,
設![]() ,
,
把![]() 代入得,
代入得, ![]() ,
,
解得![]() .
.
∴![]()
![]() .
.
(![]() )設直線AC的解析式為y=kx+b,將A、C兩點坐標代入得,
)設直線AC的解析式為y=kx+b,將A、C兩點坐標代入得,
![]() ,
,
解得 ,k=![]() ,b=4 ,
,b=4 ,
∴![]() .
.
①∠BDC=90°時,
![]() .
.
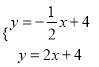 ,
, ![]() ,
,
∴![]() .
.
②∠DBC=90°時,x=-2,y=-![]() ×(-2)+4=5,則D點坐標為(-2,5);
×(-2)+4=5,則D點坐標為(-2,5);
∴![]() ,
, ![]() .
.

(3)點P在拋物線AC段上時S最大值為16,點P在拋物線AB段上時S最大值為20,
則S的取值范圍為16<S<20.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】如圖,在菱形![]() 中,
中,![]() ,
,![]() ,點
,點![]() 是
是![]() 邊的中點,點
邊的中點,點![]() 是
是![]() 邊上一動點(不與點
邊上一動點(不與點![]() 重合),延長
重合),延長![]() 交射線
交射線![]() 于點
于點![]() ,連接
,連接![]() ,
,![]() .
.

(1)求證:四邊形![]() 是平行四邊形;
是平行四邊形;
(2)填空:
①當![]() 的值為_______時,四邊形
的值為_______時,四邊形![]() 是矩形;
是矩形;
②當![]() 的值為______時,四邊形
的值為______時,四邊形![]() 是菱形.
是菱形.
查看答案和解析>>
科目:初中數學 來源: 題型:
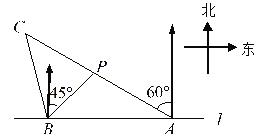
【題目】如圖,在一筆直的海岸線![]() 上有
上有![]() 、
、![]() 兩個觀測站,
兩個觀測站,![]() 在
在![]() 的正東方向,
的正東方向,![]() (單位:
(單位:![]() )有一艘小船在點
)有一艘小船在點![]() 處,從
處,從![]() 測得小船在北偏西
測得小船在北偏西![]() 的方向,從
的方向,從![]() 測得小船在北偏東
測得小船在北偏東![]() 的方向.(結果保留根號)
的方向.(結果保留根號)
(1)求點![]() 到海岸線
到海岸線![]() 的距離;
的距離;
(2)小船從點![]() 處沿射線
處沿射線![]() 的方向航行一段時間后,到達點
的方向航行一段時間后,到達點![]() 處,此時,從
處,此時,從![]() 測得小船在北偏西
測得小船在北偏西![]() 的方向,求點
的方向,求點![]() 與點
與點![]() 之間的距離.
之間的距離.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】現有一副直角三角板(角度分別為30°、60°、90°和45°、45°、90°),如圖(1)所示,其中一塊三角板的直角邊AC垂直于數軸,AC的中點過數軸原點O,AC=8,斜邊AB交數軸于點G,點G對應數軸上的數是4;另一塊三角板的直角邊AE交數軸于點F,斜邊AD交數軸于點H.
(1)如果△AGH的面積是10,△AHF的面積是8,則點F對應的數軸上的數是 ,點H對應的數軸上的數是 ;
(2)如圖(2),設∠AHF的平分線和∠AGH的平分線交于點M,若∠HAO=a,試用a來表示∠M的大小:(寫出推理過程)
(3)如圖(2),設∠AHF的平分線和∠AGH的平分線交于點M,設∠EFH的平分線和
∠FOC的平分線交于點N,求∠N+∠M的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在ABCD中,BE平分∠ABC,交AD于點E、F是BC上一點,且CF=AE,連接DF.
(1)求證:四邊形BEDF是平行四邊形;
(2)若∠ABC=70°,求∠CDF的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,![]() ,
,![]() ,試回答下列問題:
,試回答下列問題:
(1)如圖1所示,求證:![]() .
.

(2)如圖2,若點![]() 、
、![]() 在
在![]() 上,且滿足
上,且滿足![]() ,并且
,并且![]() 平分
平分![]() .求
.求![]() ________度.
________度.

(3)在(2)的條件下,若平行移動![]() ,如圖3,那么
,如圖3,那么![]() 的值是否隨之發生變化?若變化,試說明理由;若不變,求出這個比值.
的值是否隨之發生變化?若變化,試說明理由;若不變,求出這個比值.

(4)在(2)的條件下,如果平行移動![]() 的過程中,若使
的過程中,若使![]() ,求
,求![]() 度數.
度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】每年的![]() 月
月![]() 日為世界環保日,為了提倡低碳環保,某公司決定購買
日為世界環保日,為了提倡低碳環保,某公司決定購買![]() 臺節省能源的新設備,現有甲、乙兩種型號的設備可供選購.經調查:購買
臺節省能源的新設備,現有甲、乙兩種型號的設備可供選購.經調查:購買![]() 臺甲型設備比購買
臺甲型設備比購買![]() 臺乙型設備多花
臺乙型設備多花![]() 萬元,購買
萬元,購買![]() 臺甲型設備比購買
臺甲型設備比購買![]() 臺乙型設備少花
臺乙型設備少花![]() 萬元.
萬元.
(1)求甲、乙兩種型號設備每臺的價格;
(2)該公司經決定購買甲型設備不少于![]() 臺,預算購買節省能源的新設備資金不超過
臺,預算購買節省能源的新設備資金不超過![]() 萬元,你認為該公司有哪幾種購買方案;
萬元,你認為該公司有哪幾種購買方案;
(3)在(2)的條件下,已知甲型設備每月的產量為![]() 噸,乙型設備每月的產量為
噸,乙型設備每月的產量為![]() 噸.若每月要求產量不低于
噸.若每月要求產量不低于![]() 噸,為了節約資金,請你為該公司設計一種最省錢的購買方案.
噸,為了節約資金,請你為該公司設計一種最省錢的購買方案.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)請用直尺、圓規作圖,不寫作法,但要保留作圖痕跡.
已知:如圖,∠ABC,射線BC上一點D.
求作:等腰△PBD,使線段BD為等腰△PBD的底邊,點P在∠ABC內部,且點P到∠ABC兩邊的距離相等;

(2)在(1)的條件下,若∠ABC=60°,求等腰三角形△PBD頂角的度數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com