
【題目】如圖1,在平面直角坐標系xOy中,拋物線y=ax2+1經過點A(4,﹣3),頂點為點B,點P為拋物線上的一個動點,l是過點(0,2)且垂直于y軸的直線,過P作PH⊥l,垂足為H,連接PO.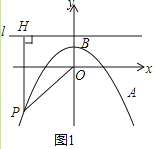
(1)求拋物線的解析式,并寫出其頂點B的坐標;
(2)①當P點運動到A點處時,計算:PO= , PH= , 由此發現,POPH(填“>”、“<”或“=”);
②當P點在拋物線上運動時,猜想PO與PH有什么數量關系,并證明你的猜想;
(3)如圖2,設點C(1,﹣2),問是否存在點P,使得以P,O,H為頂點的三角形與△ABC相似?若存在,求出P點的坐標;若不存在,請說明理由.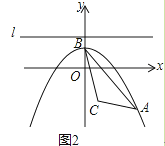
【答案】
(1)
解:∵拋物線y=ax2+1經過點A(4,﹣3),
∴﹣3=16a+1,
∴a=﹣ ![]() ,
,
∴拋物線解析式為y=﹣ ![]() x2+1,頂點B(0,1).
x2+1,頂點B(0,1).
(2)①5;5;=;②結論:PO=PH.
理由:設點P坐標(m,﹣ ![]() m2+1),
m2+1),
∵PH=2﹣(﹣ ![]() m2+1)=
m2+1)= ![]() m2+1
m2+1
PO= ![]() =
= ![]() m2+1,
m2+1,
∴PO=PH
(3)
解:∵BC= ![]() =
= ![]() ,AC=
,AC= ![]() =
= ![]() ,AB=
,AB= ![]() =4
=4 ![]()
∴BC=AC,
∵PO=PH,
又∵以P,O,H為頂點的三角形與△ABC相似,
∴PH與BC,PO與AC是對應邊,
∴ ![]() ,設點P(m,﹣
,設點P(m,﹣ ![]() m2+1),
m2+1),
∴ ![]() ,
,
解得m=±1,
∴點P坐標(1, ![]() )或(﹣1,
)或(﹣1, ![]() ).
).
【解析】(2)①當P點運動到A點處時,∵PO=5,PH=5,
∴PO=PH,
故答案分別為5,5,=.
【考點精析】本題主要考查了二次函數的性質的相關知識點,需要掌握增減性:當a>0時,對稱軸左邊,y隨x增大而減小;對稱軸右邊,y隨x增大而增大;當a<0時,對稱軸左邊,y隨x增大而增大;對稱軸右邊,y隨x增大而減小才能正確解答此題.


科目:初中數學 來源: 題型:
【題目】某中學計劃購進甲、乙兩種學具,已知一件甲種學具的進價與一件乙種學具的進價的和為40元,用90元購進甲種學具的件數與用150元購進乙種學具的件數相同.
![]() 求每件甲種、乙種學具的進價分別是多少元?
求每件甲種、乙種學具的進價分別是多少元?
![]() 該學校計劃購進甲、乙兩種學縣共100件,此次進貨的總資金不超過2000元,求最少購進甲種玩具多少?
該學校計劃購進甲、乙兩種學縣共100件,此次進貨的總資金不超過2000元,求最少購進甲種玩具多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】探究
問題1 已知:如圖1,三角形ABC中,點D是AB邊的中點,AE⊥BC,BF⊥AC,垂足分別為點E,F,AE,BF交于點M,連接DE,DF.若DE=kDF,則k的值為 .
拓展
問題2 已知:如圖2,三角形ABC中,CB=CA,點D是AB邊的中點,點M在三角形ABC的內部,且∠MAC=∠MBC,過點M分別作ME⊥BC,MF⊥AC,垂足分別為點E,F,連接DE,DF.求證:DE=DF.
推廣
問題3 如圖3,若將上面問題2中的條件“CB=CA”變為“CB≠CA”,其他條件不變,試探究DE與DF之間的數量關系,并證明你的結論.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的方程(x﹣3)(x﹣2)﹣p2=0.
(1)求證:無論p取何值時,方程總有兩個不相等的實數根;
(2)設方程兩實數根分別為x1 , x2 , 且滿足 ![]() ,求實數p的值.
,求實數p的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,下列圖形都是由相同的正方形按一定的規律組成,其中:第(1)個圖形中的正方形有2個,第(2)個圖形中的正方形有5個,第(3)個圖形中的正方形有9個,…,按此規律,則第7個圖形中的正方形的個數為_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明和小軍兩人一起做游戲,游戲規則如下:每人從1,2,…,8中任意選擇一個數字,然后兩人各轉動一次如圖所示的轉盤(轉盤被分為面積相等的四個扇形),兩人轉出的數字之和等于誰事先選擇的數,誰就獲勝;若兩人轉出的數字之和不等于他們各自選擇的數,就在做一次上述游戲,直至決出勝負.若小軍事先選擇的數是5,用列表或畫樹狀圖的方法求他獲勝的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com