
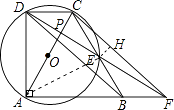
【題目】如圖,直角梯形ABCD中,AB∥CD,∠DAB=90°,且∠ABC=60°,AB=BC,△ACD的外接圓⊙O交BC于E點,連接DE并延長,交AC于P點,交AB延長線于F. 
(1)求證:CF=DB;
(2)當AD= ![]() 時,試求E點到CF的距離.
時,試求E點到CF的距離.
【答案】
(1)證明:連結AE,如圖,
∵∠ABC=60°,AB=BC,
∴△ABC為等邊三角形,
∵AB∥CD,∠DAB=90°,
∴∠ADC=∠DAB=90°,
∴AC為⊙O的直徑,
∴∠AEC=90°,即AE⊥BC,
∴BE=CE,
CD∥BF,
∴∠DCE=∠FBE,
在△DCE和△FBE中,
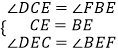 ,
,
∴△DCE≌△FBE(ASA),
∴DE=FE,
∴四邊形BDCF為平行四邊形,
∴CF=DB
(2)解:作EH⊥CF于H,如圖,
∵△ABC為等邊三角形,
∴∠BAC=60°,
∴∠DAC=30°,
在Rt△ADC中,AD= ![]() ,
,
∴DC= ![]() AD=1,AC=2CD=2,
AD=1,AC=2CD=2,
∴AB=AC=2,BF=CD=1,
∴AF=3,
在Rt△ABD中,BD= ![]() =
= ![]() ,
,
在Rt△ADF中,DF= ![]() =2
=2 ![]() ,
,
∴CF=BD= ![]() ,EF=
,EF= ![]() DF=
DF= ![]() ,
,
∵AE⊥BC,
∴∠CAE=∠BAE=30°,
∴∠EDC=∠CAE=30°,
而∠DCA=∠BAC=60°,
∴∠DPC=90°,
在Rt△DPC中,DC=1,∠CDP=30°,
∴PC= ![]() DC=
DC= ![]() ,
,
∵∠HFE=∠PFC,
∴Rt△FHE∽Rt△FPC,
∴ ![]() ,即
,即 ![]() =
= ![]() ,
,
∴EH= ![]() ,
,
即E點到CF的距離為 ![]() .
.
【解析】(1)連結AE,由∠ABC=60°,AB=BC可判斷△ABC為等邊三角形,由AB∥CD,∠DAB=90°得∠ADC=∠DAB=90°,則根據圓周角定理可得到AC為⊙O的直徑,則∠AEC=90°,即AE⊥BC,根據等邊三角形的性質得BE=CE,再證明△DCE≌△FBE,得到DE=FE,于是可判斷四邊形BDCF為平行四邊形,根據平行四邊形的性質得CF=DB;(2)作EH⊥CF于H,由△ABC為等邊三角形得∠BAC=60°,則∠DAC=30°,在Rt△ADC中,根據含30度的直角三角形三邊的關系得DC= ![]() AD=1,AC=2CD=2,則AB=AC=2,BF=CD=1,AF=3,然后利用勾股定理計算出BD=
AD=1,AC=2CD=2,則AB=AC=2,BF=CD=1,AF=3,然后利用勾股定理計算出BD= ![]() ,DF=2
,DF=2 ![]() ,所以CF=BD=
,所以CF=BD= ![]() ,EF=
,EF= ![]() DF=
DF= ![]() ,接著根據等邊三角形的性質由AE⊥BC得∠CAE=∠BAE=30°,根據圓周角定理得∠EDC=∠CAE=30°,而∠DCA=∠BAC=60°,得到∠DPC=90°,在Rt△DPC中,根據含30度的直角三角形三邊的關系得PC=
,接著根據等邊三角形的性質由AE⊥BC得∠CAE=∠BAE=30°,根據圓周角定理得∠EDC=∠CAE=30°,而∠DCA=∠BAC=60°,得到∠DPC=90°,在Rt△DPC中,根據含30度的直角三角形三邊的關系得PC= ![]() DC=
DC= ![]() ,再證明Rt△FHE∽Rt△FPC,利用相似比可計算出EH.
,再證明Rt△FHE∽Rt△FPC,利用相似比可計算出EH.


科目:初中數學 來源: 題型:
【題目】已知,如圖,在ABCD中,延長DA到點E,延長BC到點F,使得AE=CF,連接EF,分別交AB,CD于點M,N,連接DM,BN.
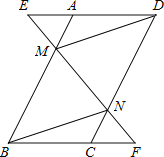
(1)求證:△AEM≌△CFN;
(2)求證:四邊形BMDN是平行四邊形.
查看答案和解析>>
科目:初中數學 來源: 題型:
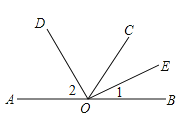
【題目】如圖,O是直線AB上的一點,C是直線AB外的一點,OD是∠AOC的平分線,
OE是∠COB的平分線.
(1)已知∠1=23°,求∠2的度數;
(2)無論點C的位置如何改變,圖中是否存在一個角,它的大小始終不變(∠AOB除外)?如果存在,求出這個角的度數;如果不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】合并下列多項式中的同類項:
(1)3x2+4x﹣2x2﹣x+x2﹣3x﹣1;
(2)﹣a2b+2a2b;
(3)a3﹣a2b+ab2+a2b﹣2ab2+b3;
(4)2a2b+3a2b﹣![]() a2b
a2b
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,二次函數y= ![]() x2+bx+c的圖象與x軸交于A(3,0),B(﹣1,0),與y軸交于點C.若點P,Q同時從A點出發,都以每秒1個單位長度的速度分別沿AB,AC邊運動,其中一點到達端點時,另一點也隨之停止運動.
x2+bx+c的圖象與x軸交于A(3,0),B(﹣1,0),與y軸交于點C.若點P,Q同時從A點出發,都以每秒1個單位長度的速度分別沿AB,AC邊運動,其中一點到達端點時,另一點也隨之停止運動.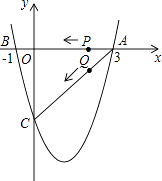
(1)求該二次函數的解析式及點C的坐標;
(2)當點P運動到B點時,點Q停止運動,這時,在x軸上是否存在點E,使得以A,E,Q為頂點的三角形為等腰三角形?若存在,請求出E點坐標;若不存在,請說明理由.
(3)當P,Q運動到t秒時,△APQ沿PQ翻折,點A恰好落在拋物線上D點處,請判定此時四邊形APDQ的形狀,并求出D點坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,三角形ABC三個頂點A,B,C的坐標分別為A(1,2),B(4,3),C(3,1).
(1)三角形A1B1C1向右平移4個單位長度,再向下平移3個單位長度,恰好得到三角形ABC,試寫出三角形A1B1C1三個頂點的坐標.
(2)求△ABC的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】畫圖并計算:已知線段AB=2 cm,延長線段AB至點C,使得2BC=AB,再反向延長AC至點D,使得AD=AC.
(1)準確地畫出圖形,并標出相應的字母;
(2)線段DC的中點是哪個?線段AB的長是線段DC長的幾分之幾?
(3)求出線段BD的長度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC是邊長為6的等邊三角形,P是AC邊上一動點,由A向C運動(與A、C不重合),Q是CB延長線上一點,與點P同時以相同的速度由B向CB延長線方向運動(Q不與B重合),過P作PE⊥AB于E,連接PQ交AB于D. 
(1)當∠BQD=30°時,求AP的長;
(2)當運動過程中線段ED的長是否發生變化?如果不變,求出線段ED的長;如果變化請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com